В микроэкономике используется большое количество производственных функций, но особую популярность занимает функция Кобба-Дугласа, отражающая зависимость объема производства от используемых факторов производства (капитала и труда) и имеет вид:
где:
![]()
![]() – объем производства,
– объем производства,
![]()
![]() – капитал,
– капитал,
![]()
![]() – труд,
– труд,
![]()
![]() – масштабное число,
– масштабное число,
![]()
![]() – показатель эластичности по труду,
– показатель эластичности по труду,
![]()
![]() – показатель эластичности по капиталу.
– показатель эластичности по капиталу.
Причем, ![]()
![]() ,
, ![]()
![]() .
.
Показатели описывают насколько процентов изменяется выпуск при изменении капитала или труда на один процент.
Для нахождения параметров ![]()
![]() используем статистические данные ПАО «Новолипецкий металлургический комбинат», которые отражены в таблице 1.
используем статистические данные ПАО «Новолипецкий металлургический комбинат», которые отражены в таблице 1.
Таблица 1. Статистические данные ПАО «Новолипецкий металлургический комбинат».
| Год | L – Рабочая сила, тыс. чел. | К – Капитал, млн. долл. | Y – Выручка, млн. долл. |
| 2004 | 52,5 | 2258 | 4539 |
| 2005 | 52,5 | 2394 | 4469 |
| 2006 | 70,8 | 3988 | 6046 |
| 2007 | 60,2 | 6449 | 7719 |
| 2008 | 70,1 | 6826 | 11698 |
| 2009 | 62,8 | 7316 | 6139 |
| 2010 | 59,3 | 8382 | 8351 |
| 2011 | 60,4 | 10596 | 11729 |
| 2012 | 62,5 | 11753 | 12157 |
| 2013 | 62,1 | 10002 | 10818 |
| 2014 | 60,1 | 5866 | 10396 |
| 2015 | 61,1 | 7965 | 8008 |
Для построения производственной функции Кобба-Дугласа необходимо найти параметры ![]()
![]() . Будем использовать метод наименьших квадратов. Тогда задача будет выглядеть следующим образом:
. Будем использовать метод наименьших квадратов. Тогда задача будет выглядеть следующим образом:
При ограничениях:
Где ![]()
![]() – отклонение расчетного значения от фактического (
– отклонение расчетного значения от фактического (![]()
![]() ).
).
Были получены следующие значения:
Тогда производственная функция Кобба-Дугласа в нашем случае принимает вид:
Для анализа производственной функции Кобба-Дугласа ![]()
![]() построим изокванты, соответствующей выпуску
построим изокванты, соответствующей выпуску ![]()
![]() и построим их график с помощью MS Excel (Рисунок 1. Изокванты для функции Кобба-Дугласа).
и построим их график с помощью MS Excel (Рисунок 1. Изокванты для функции Кобба-Дугласа).
Изокванта показывает все комбинации двух факторов производства (капитала и труда) при которых выпуск остается неизменным.
Уравнение изокванты будет иметь вид:
![]()
Для построения первой изокванты возьмем выпуск равный![]()
![]() млн. долл. и найдем
млн. долл. и найдем ![]()
![]() как функцию от
как функцию от ![]()
![]() :
:
![]()
Аналогично можно построить изокванты для ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() выпусков.
выпусков.
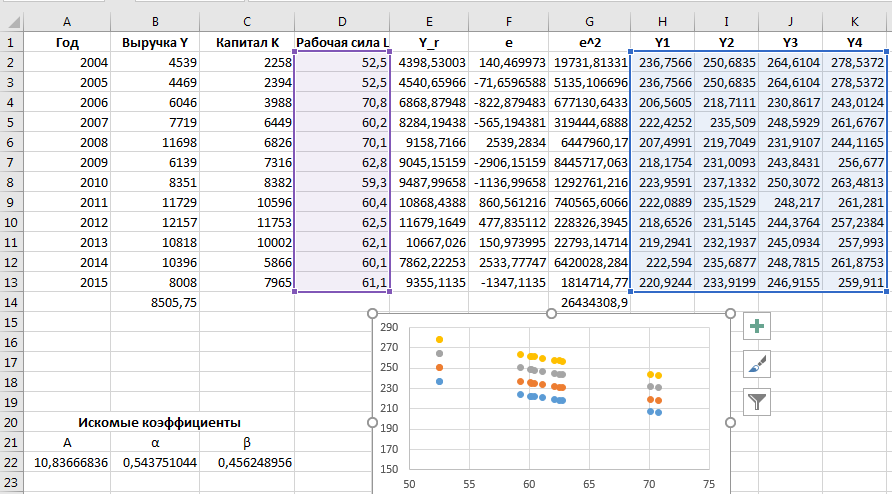
Рисунок 1. Изокванты для функции Кобба-Дугласа.
Для производственной функции Кобба-Дугласа покажем, что эластичность выпуска по капиталу равна показателю степени при капитале.
Эластичность выпуска по ![]()
![]() -ому ресурсу является отношение предельной производительности
-ому ресурсу является отношение предельной производительности ![]()
![]() -ого ресурса к средней производительности. Эластичность характеризует процент прироста объема выпуска продукции при увеличении затрат ресурсов на 1%.
-ого ресурса к средней производительности. Эластичность характеризует процент прироста объема выпуска продукции при увеличении затрат ресурсов на 1%.
.gif)

Вывод: была построена производственная функция Кобба-Дугласа ![]()
![]() по реальным статистическим данным, используя метод наименьших квадратов. Функция Кобба-Дугласа для данной задачи принимает вид:
по реальным статистическим данным, используя метод наименьших квадратов. Функция Кобба-Дугласа для данной задачи принимает вид:
Доля капитала в совокупном продукте составляет 54%, а доля труда – 46%. При увеличении рабочей силы на 1% выпуск увеличится на 0,54%, а при увеличении капитала на 1% выпуск увеличится на 0,46%. Можно отметить, что в 2004-2015 гг. наблюдался экстенсивный рост, так как показатель ![]()
![]() .
.
В данной работе также построены изокванты для производственной функции Кобба-Дугласа, и показано, что эластичность выпуска по капиталу равна показателю степени при капитале.
Библиографический список
- Галиаскарова Г. Р. Практикум по математической экономике. Учебное пособие для студентов. – Уфа: РИЦБашГУ, 2011.-88с.
- Годовые отчеты ПАО «НЛМК», http://nlmk.com/ru/
