В настоящее время многочисленные фонды привлекают средства населения, рекламируя различные стратегии управления этими средствами. При этом позитивные результаты работы по этим стратегиям приводятся, как правило, за сравнительно небольшой промежуток времени. Неквалифицированный инвестор часто не может самостоятельно оценить риски дальнейшей работы по этим стратегиям. В то же время опытные инвесторы, как правило, индивидуалисты, могут на основании обмена опытом создавать более эффективные стратегии. Проблемой является то, что механизмы агрегирования индивидуальных стратегий обычно ограничены различными вариантами линейных комбинаций портфелей [1]. Настоящая статья, наряду с [2], создаёт предпосылки для конструирования более сложных механизмов агрегирования.
Рассматриваются простейшие индивидуальные системы принятия инвестиционных решений, формирующие на основе предшествующей динамики цены единственного актива одно из трех состояний инвестиционного портфеля:1. Long – прибыль возникает при увеличении цены актива;
2. Out – вне позиции, никаких действий не совершается.
3. Short – прибыль образуется при снижении цены актива;Формирование позиции агрегированной системы предлагается производить на основе голосования (возможно, асимметричного) среди индивидуальных систем. Пример матрицы агрегирования, определяющей результат такого голосования для случая двух индивидуальных систем, приведен в Таблице 1.

Таблица 1 – Пример матрицы агрегирования

		Первая система
		Long	Out	Short
Вторая система	Long	Long	Out	Out
	Out	Long	Out	Out
	Short	Out	Short	Short

Очевидно, что при объединении трёх исходных систем в одну агрегированную, логика выбора позиции агрегированной системы усложняется. В то же время появляется большое число очевидных предпочтений при выборе. Во всех случаях целесообразность объединения систем диктуется наличием синергетического эффекта, когда агрегированная система даёт лучшие результаты, чем индивидуальные системы в сумме.
Условием получения синергетического эффекта при объединении всех индивидуальных систем является существование непустого С-ядра соответствующей кооперативной игры [3, c.165].
Рассмотрим пример нахождения C-ядра при агрегировании трёх индивидуальных систем A, B, C. Пусть за выбранный промежуток времени показатели прибыли составили, соответственно, V(A)=3%, V(B)=1,5%, V(C)=0,6%. Очевидно, что при существовании синергетического эффекта от объединения, эффективность (X_A, X_B, X_C) каждой из индивидуальных систем в составе агрегированной должна быть не ниже, чем при ее индивидуальном использовании. Для этого значения X_A, X_B, X_C должны удовлетворять системе неравенств (1):
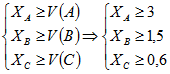(1)

Если прибыль агрегированной системы V(ABC) составила 9%, а при агрегировании систем попарно определились прибыли: V(AB)=5,4%; V(AC)=4,5%;V(BC)=3%, то систему (1) можно дополнить следующими ограничениями:

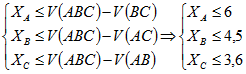(2)

Предполагая, что вся прибыль должна быть поделена между участниками, получим:

(3)

Геометрически (1)-(3) определяют плоский многоугольник (заштрихованная область на рис.1) в трёхмерном пространстве (C-ядро), любая точка которого определяет приемлемый дележ прибыли между индивидуальными системами:

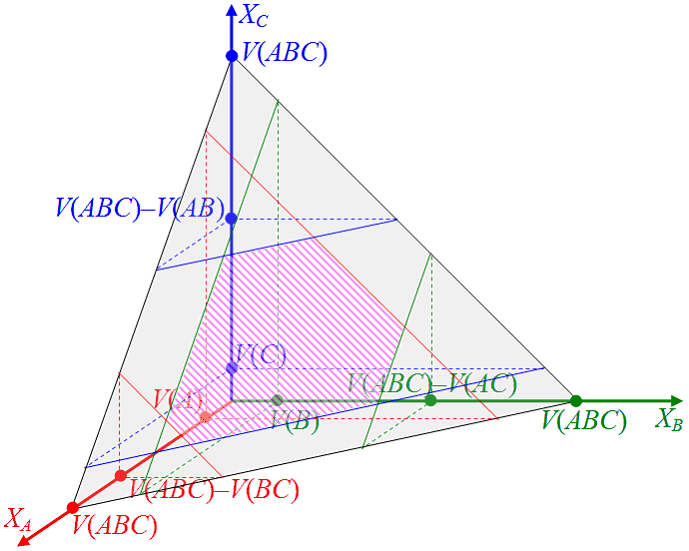
Рисунок 1. Формирование С-ядра

Запас устойчивости синергетического эффекта агрегированной системы можно ассоциировать с некоторой мерой на множестве возможных многоугольников С-ядра, например, с площадью многоугольника. Восстановление запаса устойчивости осуществляется изменением матрицы агрегирования. В случае, когда запас устойчивости стремится к нулю, то есть C-ядро оказывается пустым, возможно, что одна из пар индивидуальных систем формирует непустое C-ядро и для этой пары синергетический эффект присутствует.
Если С-ядро непустое и содержит множество возможных дележей, то возникает вопрос выбора наилучшего дележа. Одним из способов выбора справедливого дележа является формирование вектора Шепли [3, c.173]. Этот дележ определяется по следующей схеме.
На первом этапе рассматривается последовательное агрегирование систем в следующей последовательности: A, AB, ABC. На каждого варианта определяется прибыль: V(A), V(AB), V(ABC). Затем определяются приращения прибыли, вызванные добавлением каждой из индивидуальных систем:V(А), V(AB)–V(A); V(ABC)–V(AB). Аналогично рассматриваются все возможные последовательности добавления индивидуальных систем. Приведённый метод вычисления дополнительных прибылей позволяет сформировать следующую таблицу:

Таблица 2 – Дополнительные прибыли для расчета вектора Шепли

Находя среднее арифметическое в каждом столбике, получим среднюю прибыль, привносимую каждой из индивидуальных систем при агрегировании. Эта средняя прибыль и является выплатой инвестору по методу Шепли.
Далее возвращаемся к нашему примеру и подсчитываем прибыли каждого инвестора. Сформируем таблицу по описанному выше принципу:

Таблица 3 – Пример расчета вектора Шепли

Общая прибыль в 9% будет распределена следующим образом: прибыль первого инвестора составит 4,23%, второго – 2,73%, третьего – 2,03% от общей суммы вложений.
Таким образом в статье рассмотрен ряд вопросов связанных с формированием агрегированной системы коалиции инвесторов, выполнением условий при которых возникает синергетический эффект при её использовании, определением запаса устойчивости агрегированной системы в процессе её эксплуатации, способом изменения структуры этой системы и распределения возникающей прибыли (убытков) между инвесторами.

1. Титов С.Ю. Адаптивная система принятия решений на финансовых рынках // Прикладная эконометрика. – 2007. – №3(7). – С. 27-43
2. Саркисов В.Г., Саркисов Г.А. Синтез системы управления инвестиционным портфелем на основе моделирования виртуальных финансовых инструментов // Вестник Самарского государственного технического университета. Серия: Технические науки. 2011. № 3 (32). С. 33-39.
3. Петросян Л.А., Зенкевич Н.А., Шевкопляс Е.В. Теория игр / СПб.: БХВ-Петербург, 2012 – 432 с.

Все статьи автора «Саркисов Виген Геннадьевич»