Научный руководитель: доктор экономических наук, профессор Бакуменко Людмила Петровна
Объектом исследования в данной работе являются социально-экономические показатели регионов России за 2016 год [6].
За последнее десятилетие анализ многомерных данных стал одним из основных направлений прикладной математики, активно развивающимся и применяющимся практически во всех областях исследований, в том числе и в территориальных исследованиях.
Факторный анализ трактуется как раздел многомерного статистического анализа, объединяющий методы оценки размерности множества наблюдаемых переменных посредством исследования структуры ковариационных или корреляционных матриц.
Данный вид анализа позволяет исследователю решить две основные задачи: описать предмет измерения компактно и в то же время всесторонне. С помощью факторного анализа возможно выделение факторов, отвечающих за наличие линейных статистических связей корреляций между наблюдаемыми переменными [4].
Для выявления наиболее значимых факторов и, как следствие, факторной структуры, наиболее оправданно применять метод главных компонентов. Следовательно, метод главных компонент оказывается весьма ценным инструментом территориальных исследований, поскольку дает возможность выявить и типичные сочетания некоторых региональных параметров, характерных для большинства субъектов РФ, и особенности, присущие лишь немногим регионам. Другой важной характеристикой метода является возможность ограничиться наиболее информативными главными социально-экономическими компонентами и исключить остальные из анализа, что упрощает интерпретацию результатов.
В данной работе рассматривается численность населения и 12 социально-экономических показателей по 85 регионам России.
Для установления связи между численностью населения и социально-экономическими показателями предлагается использовать модели, построенные на основе главных компонент. Метод главных компонент применяется для группировки исходных факторов таким образом, чтобы члены группы обладали корреляцией между собой, но группа в целом была бы независима от других групп. Линейно независимые группы факторов называют главными компонентами [2].
В начале анализа рассмотрим собственные значения, представленные в таблице 1.
Таблица 1 – Собственные значения
|
Собственные значения (Таблица данных1) Выделение: Главные компоненты |
||||
|
Соб. зн. |
% общей |
Кумулятивн. |
Кумулятивн. |
|
|
1 |
3,982823 | 33,19019 | 3,982823 | 33,19019 |
|
2 |
2,204457 | 18,37048 | 6,187280 | 51,56067 |
|
3 |
1,114099 | 19,28416 | 7,301379 | 70,84483 |
|
4 |
1,068120 | 11,90100 | 8,369499 | 82,74583 |
Дисперсии, выделяемые факторами, названы собственными значениями. В третьей колонке для каждого фактора приводится процент от общей дисперсии. Исходя из таблицы 1, первый фактор (значение 1) объясняет 33,2% общей дисперсии, фактор 2 – 18,4%. После получения информации о том, сколько дисперсии выделяет каждый фактор, нужно определить, какие факторы стоит оставлять.
Для группировки исходных факторов по независимым группам в методе главных компонент необходимо произвести отбор числа факторов. Для этого используются такие критерии как:
-
Критерий Кайзера: в рассмотрение принимаются только факторы, которым соответствуют собственные числа ковариационной матрицы больше 1.
-
Критерий каменистой осыпи: отбрасываем все факторы, соответствующие собственные числа которых мало отличаются.
В общем же случае приходится ограничиваться последовательной эксплуатацией критериев адекватности H0: m = m0 при альтернативе H1: m > m0 . Если гипотеза H0 отвергается, то переходят к проверке гипотезы: H0′: m’ = m0 +1 при альтернативе H1′: m’ = m0 +1и т.д. Однако по уровням значимости у каждой отдельной стадии такой процедуры трудно судить о свойствах всей последовательной процедуры в целом [5].
Для отбора социально-экономических факторов воспользуемся критерием каменистой осыпи. Построим график каменистой осыпи, представленный на рисунке 1. По нему видно, что осыпание наиболее существенно замедляется на четвертой точке, следовательно, можно ограничиться четырьмя факторами.
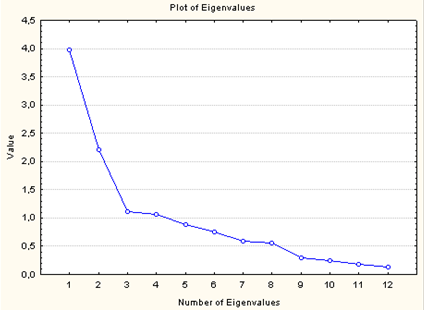
Рисунок 1 – График каменистой осыпи
В результате получаем 4 главные компоненты, у которых собственные значения больше 1.
Определим факторные нагрузки, выделим переменные, которые коррелируются с главной компонентой от 0,7. Факторные нагрузки можно интерпретировать как корреляции между факторами и переменными. Поэтому они представляют наиболее важную информацию, на которой основывается интерпретация факторов. В таблице 2 представлены факторные нагрузки для всех 4 факторов до вращения.
Таблица 2 – Факторные нагрузки без вращения
| Фактор.нагрузки (без вращения) (Таблица данных1) Выделение: Главные компоненты (Отмечены нагрузки >,700000) | ||||
|
Фактор 1 |
Фактор 2 |
Фактор 3 |
Фактор 4 |
|
| x1 |
-0,792718 |
-0,015306 |
-0,236657 |
0,231022 |
| x2 |
-0,720889 |
-0,253469 |
-0,425446 |
0,000304 |
| Продолжение таблицы 2 | ||||
| x3 |
-0,639370 |
0,227029 |
-0,414539 |
-0,361765 |
| x4 |
-0,384959 |
-0,302679 |
-0,187281 |
-0,493861 |
| x5 |
-0,588400 |
-0,513302 |
0,220713 |
0,160251 |
| x6 |
-0,432975 |
-0,062541 |
0,269077 |
0,081812 |
| x7 |
-0,425085 |
-0,626695 |
0,418024 |
0,270069 |
| x8 |
0,643091 |
0,492280 |
-0,293831 |
0,053923 |
| x9 |
-0,396616 |
0,739432 |
0,410269 |
-0,176563 |
| x10 |
-0,667439 |
0,245035 |
-0,192070 |
0,240450 |
| x11 |
0,041526 |
0,398202 |
-0,303857 |
0,695181 |
| x12 |
-0,705614 |
0,502615 |
0,052021 |
-0,033289 |
| Общ.дис. |
4,061986 |
2,762502 |
1,269428 |
1,110508 |
| Доля общ |
0,312460 |
0,212500 |
0,097648 |
0,085424 |
Из таблицы 2 видно, что два последних фактора оказались не загруженными, следовательно, необходимо произвести вращение факторов. Возможен выбор различный поворот оси. Выберем вращение квартимах исходный, то есть вращаемые нагрузки не нормализированы [3].
Получаем график факторных нагрузок, представленный на рисунке 2.
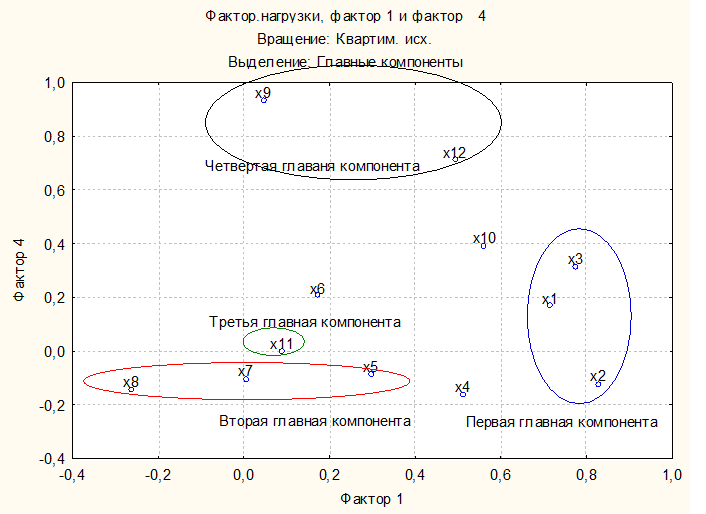
Рисунок 2 – Факторные нагрузки
Далее формируем главные компоненты. Первая главная компонента коррелирует со следующими показателями:
-
X1 – Число браков на 1000 человек населения;
-
X2 – Число разводов на 1000 человек населения;
-
Х3 – Уровень занятости, в %.
Поэтому данную компоненту назовем брачная составляющая.
Вторая главная компонента коррелирует с переменными:
-
Х5 – Число зарегистрированных преступлений на 100000 человек населения;
-
X7 – Лесистость территорий, %;
-
X8 – Земельная площадь с/х угодий в % от общей площади.
Обобщая, можно сказать, что вторая главная компонента отражает число правонарушений и отражает состояние экологии на территории регионов. Совокупность выделенных параметров характеризует уровень преступности и экологии, поэтому данную компоненту назовем составляющая преступности и экологии.
Третья главная компонента коррелирует с переменной X11 – Ввод в действие жилых домов на 1000 человек населения, м2 общей площади. Поэтому назовем ее жилищной составляющей.
Четвертая главная компонента коррелирует с переменными:
-
X9 – Число предприятий и организаций;
-
X12 – Оборот розничной торговли на душу населения, рублей.
Данная компонента выражает уровень развития бизнеса и торговли, поэтому назовем ее бизнес составляющей.
Рассчитаем коэффициент информативности главных компонент. Получаем таблицу 3 с факторными нагрузками.
Таблица 3 – Факторные нагрузки после вращения
| Фактор.нагрузки (Квартим. исх.) (Таблица данных1) Выделение: Главные компоненты (Отмечены нагрузки >,700000) | ||||
|
Фактор 1 |
Фактор 2 |
Фактор 3 |
Фактор 4 |
|
| x1 |
0,715929 |
0,360501 |
0,256623 |
0,168966 |
| x2 |
0,82679 |
0,295679 |
0,007606 |
-0,118974 |
| x3 |
0,774476 |
-0,128775 |
-0,195734 |
0,318702 |
| x4 |
0,510802 |
0,121441 |
-0,509201 |
-0,16029 |
| x5 |
0,296106 |
0,770629 |
-0,039521 |
-0,083861 |
| x6 |
0,172929 |
0,407124 |
0,020726 |
0,206114 |
| Продолжение таблицы 3 | ||||
| x7 |
0,00424 |
0,904555 |
-0,013172 |
-0,100703 |
| x8 |
-0,262511 |
-0,780591 |
0,254926 |
-0,141881 |
| x9 |
0,045929 |
-0,078405 |
-0,025454 |
0,935688 |
| x10 |
0,561755 |
0,174611 |
0,330082 |
0,395582 |
| x11 |
0,089359 |
-0,224129 |
0,829483 |
0,002877 |
| x12 |
0,491379 |
0,073593 |
0,110398 |
0,713149 |
| Общ.дис. |
2,810498 |
2,528164 |
1,240495 |
1,790342 |
| Доля общ |
0,234208 |
0,21068 |
0,103375 |
0,149195 |
| К. инф. |
0,639015 |
0,799557 |
0,554651 |
0,773089 |
Как видно из таблицы 3, фактор 2 (составляющая преступности и экологии) имеет наибольшую информативность, а значит, он оказывает наибольшее влияние на численность населения. Наименьшую информативность имеет жилищная составляющая.
О нормальности остатков также можно судить по вероятностному графику остатков, который представлен на рисунке 3.
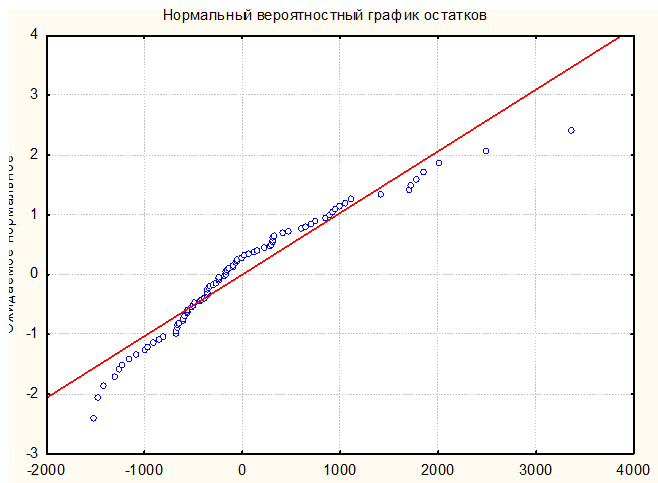
Рисунок 3 – Нормальный вероятностный график остатков
Так как остатки достаточно хорошо ложатся на прямую, то можно говорить о том, что распределение близко к нормальному и разделение по компонентам выполнено правильно.
Следовательно, основными факторами, влияющими на численность населения в России, являются: брачная составляющая, составляющая преступности и экологии, жилищная составляющая и бизнес составляющая. Причем составляющая преступности и экологии оказывает наибольшее влияние на численность населения регионов России.
Библиографический список
- Бородич, С.А. Вводный курс Эконометрики: Учебное пособие [Текст]/С.А. Бородич – Мн.: БГУ, 2013. – 354 с.
- Буреева, Н.Н. Многомерный статистический анализ с использованием ППП “STATISTICA”. Учебно-методический материал по программе повышения квалификации «Применение программных средств в научных исследованиях и преподавании математики и механики» [Текст]/ Н.Н. Буреева – Нижний Новгород, 2013, 112 с.
- Колемаев В. А. Эконометрика : учеб. для студентов вузов по специальности 061800 “Мат. методы в экономике” / В. А. Колемаев ; М-во образования РФ, Гос. ун-т упр. – М. : ИНФРА-М, 2014. – 160 с.
- Крамер, Н.Ш., Путко, Б.А. Эконометрика: Учебник для вузов [Текст]/ Под рек. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2012. – 311 с.
- Эконометрика: учет./под ред.. И. И. Елисеевой. – М.: Проспект, 2014. – 228 с.
- GKS [Электронный ресурс]. – Режим доступа: http://www.gks.ru
