Научный руководитель: Бакуменко Людмила Петровна
Поволжский государственный технологический университет, доктор экономических наук

Уровень здоровья населения относится к числу наиболее значимых направлений исследования в социальной статистике. Это важный показатель, который требует особо четкого внимания. 
Для того чтобы понять настоящую ситуацию в этой сфере, необходим ежегодный мониторинг данной области. Но так как простого сбора данных недостаточно, то нужен их анализ, а также установление различных взаимосвязей и выявление факторов, влияющих на те или иные показатели. 
Таким образом, уровень заболеваемости является одной из основных социальных проблем, которая главным образом влияет в целом на число населения.
Для анализа и обработки огромного количества регистрируемых признаков, необходимо воспользоваться удобным и четким методом главных компонент, он предполагает уменьшение размерности информации. 
Ниже приведены факторы, которые влияют на заболеваемость девочек 14-16 лет. Проанализируем данные Минздрава России за 2016 год. 
x₁ - группа заболеваний, вызываемых паразитами, а также инфекционные заболевания, чел.;
x₂ -  болезни системы крови, кроветворных органов и иммунного механизма, чел.; 
x₃ -  нарушения пищевого поведения и нарушения углеводного обмена, чел.; 
x₄ -  расстройства поведения и душевные расстройства, чел.;
x₅ -  нервные заболевания, чел.;
x₆ -  глазные заболевания, чел.;
x₇ -  ушные заболевания, чел.;
x₈ -  болезни системы кровообращения, чел.;
x₉ -  заболевания органов дыхания, чел.;
x₁₀ -  болезни органов пищеварения, чел.;
x₁₁ -  кожные заболевания, чел.; 
x₁₂ -  болезни мочеполовой системы, чел.;
x₁₃ -  последствия внешних причин (травмы), чел.;
Проанализируем данные Минздрава России за 2016 год. Для этого необходимо сформировать главные компоненты путем выделения наиболее значимых факторов и построить уравнения регрессии на главных компонентах. Метод главных компонент необходимо применить к исходным данным, реализуемым в прикладной программе STATISTICA с помощью пакета «Факторный анализ» (Многомерный разведочный анализ). Полученные собственные значения отражены в таблице 1.

Таблица 1 – Собственные значения

С помощью МГК было выделено всего 2 фактора. В данном случае 68,28%  общей дисперсии объясняется первым фактором, 7,97% – вторым фактором, Вместе все факторы объясняют 76% дисперсии.

Далее необходимо оценить значения факторных нагрузок и вычислить коэффициенты информативности для случая с двумя факторами. Главная компонента считается информативной, если коэффициент достаточно высокий Ки ≥ 0,65 ÷ 0,95. Исходя из условия информативности, только первые два фактора являются информативными, поэтому необходимо использовать вращения для факторных нагрузок. В результате после применения вращения «Варимакс исходных», получаем более высокие коэффициенты информативности у первого и второго факторов, это представлено в таблице 2.

Таблица 2 – Факторные нагрузки при варимакс исходных

При варимакс исходных коэффициенты информативности получаются достаточно хорошими для двух факторов, поэтому нет необходимости уменьшать количество факторов.
Переменные, которые вошли в каждую главную компоненту. 
К первой компоненте относятся: x₁ - группа заболеваний, вызываемых паразитами, а также инфекционные заболевания.; x₃ - нарушения пищевого поведения и нарушения углеводного обмена; x₅ -  нервные заболевания, чел; x₆ - глазные заболевания; x₇ - ушные заболевания; x₉ - заболевания органов дыхания; x₁₀ - болезни органов пищеварения; x₁₁ - кожные заболевания; x₁₂ - болезни мочеполовой системы; x₁₃ - последствия внешних причин (травмы). 
Ко второй компоненте относится x₄ - расстройства поведения и душевные расстройства, чел.;
Далее необходимо определить степень влияния каждого фактора на результативный признак y - число заболеваний, зарегистрированных у девочек 14-16 лет. Выведенная пошаговая регрессия с исключением представлена в таблице 3.

Таблица 3 – Итоги множественной регрессии

Отсюда следует, что значимым является только первый фактор. Полученное уравнение регресии имеет вид:

      (1)

Коэффициент детерминации R² =0,97 показывает, что 97% вариации результативного признака объясняется включенной в модель переменной (фактор 1), остальные 3% вариации объясняется неучтёнными в модели факторами.

Модель можно считать значимой, так как фактическое значение F- критерия Фишера превышает критическое при заданных степенях свободы и уровне значимости 97%.

Каждый коэффициент также можно считать значимым, так как критическое значение t-критерия Стьюдента меньше каждого фактического значения.
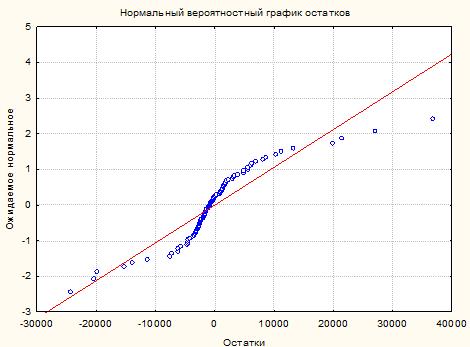
По вероятностному графику, который изображен на рисунке 1, видно, что значения остатков распределены достаточно равномерно и хорошо ложатся на график нормальных остатков.

Рисунок 1  Нормальный вероятностный график

Коэффициенты уравнения показывают, насколько изменится значение результативного признака при изменении величины факторного на 1 единицу. С уменьшением показателя f₁ на 1 единицу значение результативного признака уменьшится на 45283,8 ед. Влияние показателя f₂ оказалось незначительным и не вошло в окончательное уравнение.
Из уравнения видно, что первый фактор наиболее часто встречается как заболевание, зарегистрированное у девочек 14-16 лет. 
Можно сделать вывод, что в ходе данной работы были выделены две главные компоненты, что облегчило дальнейшую работу с моделью. Затем с помощью пошаговой регрессии с исключением были выделены наиболее существенные факторы и объяснено их влияние на результативный признак.

1. Алексеев А.Р. Экономическая статистика: учебник для вузов / [Алексеев А.Р., Воробьев А.Н., Громыко Г.Л., и др.]; под ред. Ю.Н. Иванова. – М.: ИНФРА-М, 2014. – 734 с.
2. Бабешко Л.О. Основы эконометрического моделирования : учеб. пособие / Л. О. Бабешко. – Изд. 4-е. – М.: КомКнига, 2013. – 428 с.
3. Дианов М.А., Никитина С.Ю.  Здравоохранение в России. 2015: Стат.сб./Росстат. – М., З–46 2015. – 174 с.
4. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2013. – 311 с.
5. Костромин А.В., Кундакчян Р.М.  Эконометрика. Учебное пособие / Издательство: Кнорус, 2015 г., – 228с.
6. Статистический сборник «Регионы России. Социально экономические показатели», 2013. Федеральная Служба Государственной Статистики.
7. Статистические методы прогнозирования, Дуброва Т.А., 2015.

Все статьи автора «Шувалов Николай Евгеньевич»