Среди применяемых методов моделирования важное место занимают экономико-математические методы, которые применяются для решения следующих практических задач:
Совершенствование системы экономической информации для бюджетного планирования: оптимизация регистрации учета информационной системы, выявление недостатков в имеющейся информации и разработка требований к подготовке новой информации или обновлении информации.
Интенсификация и повышение точности балансовых расчетов и прогнозов расходов и доходы.
Углубление количественного анализа процессов формирования и использования бюджетных средств, количественная оценка последствий спецификация и перераспределение сметных расходов в условиях изменяющихся предметов и т. д.
Решение принципиально новых задач бюджетного планирования, формирования и управления.
Характеристики модели бюджета:
Модель работает с данными из одного финансового года;
Ввод данных: прогнозные значения доходов и расходов по отношению к расчетной базе объектов бюджетной системы;
Выходные данные: бюджет проекта близко к реальному исполнению;
Влияние внешних факторов на системы – изменения планируемых поступлений и расходов;
Результат работы модели—возможность регулирования бюджета проекта в соответствии с реальным исполнением.
Пусть m-количество элементов дохода, из которых формируется бюджет, и
n - количество статей расходов, по которым бюджет должен быть распределен. Исходя из предположения о пропорциональном распределении каждой единицы дохода среди всех статей расходов, введем коэффициент, отражающий долю каждого элемента дохода в данной статье расходов:
![]() (1.1)
(1.1)
где ![]() - абсолютное значение i-й статьи расходов;
- абсолютное значение i-й статьи расходов;
![]() - абсолютное значение j-го дохода;
- абсолютное значение j-го дохода;
![]() – коэффициент взаимодействия доходов и расходов.
– коэффициент взаимодействия доходов и расходов.
Коэффициенты взаимодействия можно рассматривать как:
- распределение элемента дохода
- формирование расходов
С точки зрения формирования каждого фиксированного i-го элемента расходов (включая все статьи доходов), имеем:
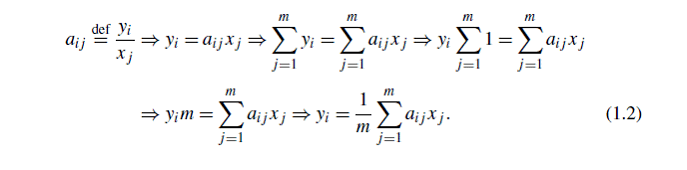

В матричной форме связь между доходами и расходами статей можно записать в виде:

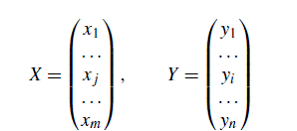

где А - является матрицей взаимодействий между доходных и расходных статей размера n Ч m.
Матрица А представляет собой компактный носитель данных, содержащий данные о внутреннем состоянии системы и принципы распределения бюджетных средств по статьям расходов. Одно из состояний матрицы А может быть использовано в качестве идеального варианта планирования бюджета.
Основным принципом бюджетной системы является то, что бюджет государства должен быть сбалансирован для любого уровня бюджетной классификации:
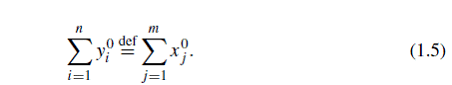
Согласно этому принципу, матрица взаимодействия должна привести к сбалансированному состоянию пункта бюджета и сохранить его во всех возможных регулировок потока.
Пусть векторы X0 и Y0 характеризуют сбалансированное состояние бюджета. Согласно (1.4), мы имеем:

или в координатной форме

где 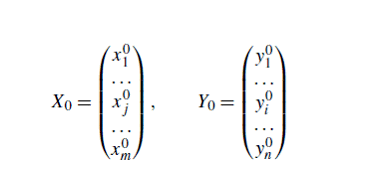 являются, соответственно, векторами доходов и расходов для сбалансированного состояния бюджета; m - это количество статей бюджета; и
являются, соответственно, векторами доходов и расходов для сбалансированного состояния бюджета; m - это количество статей бюджета; и ![]() матрица взаимодействий, приводящий бюджет в сбалансированное состояние.
матрица взаимодействий, приводящий бюджет в сбалансированное состояние.
С точки зрения распределения каждого фиксированного j-го дохода среди всех статей расходов, ![]() , имеем:
, имеем:
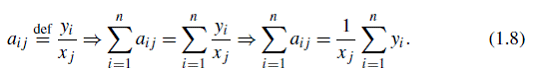
Равенство (1.13) справедливо и для ситуации баланса:
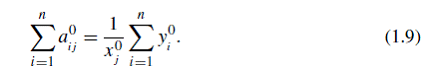
Равенства (1.9) и (1.5) позволяют сделать вывод: сумма элементов j-го столбца матрицы баланса взаимодействия равно отношению всех сбалансированных бюджетов дохода к доходу j-го элемента.
На самом деле, для сбалансированного состояния бюджета элементов матрицы взаимодействия ![]()
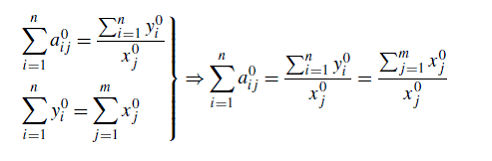
откуда (с теми же обозначениями) мы имеем:

Очевидным следствием (1.10) является утверждение, что каждый i-й элемент сбалансированного бюджета является отношением самого сбалансированного бюджета на сумму коэффициентов взаимодействия для всех статей расходов, среди которых j-й был распространен как:
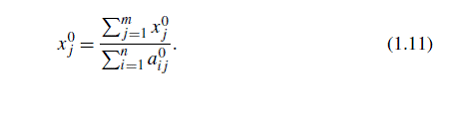
Рассмотрим сумму запланированных акций бюджета:
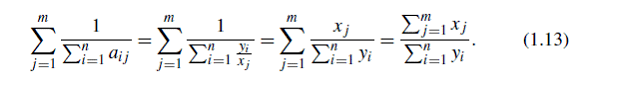
Для следующих вариантов государственного бюджета как: баланс, профицит и дефицит. Согласно (1.13) имеем:
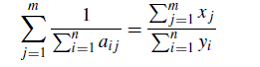
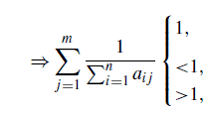

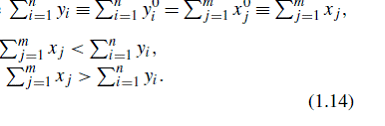
Следовательно, (1.14) может быть использована для анализа состояния бюджета:
если ![]() , для сбалансированного государственного бюджета
, для сбалансированного государственного бюджета
если ![]() , для дефицитного государственного бюджета, и дефицитная доля это:
, для дефицитного государственного бюджета, и дефицитная доля это:
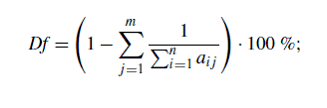
если 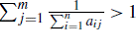 , для профицитного (или избыточного) государственного бюджета, и профицитная доля это:
, для профицитного (или избыточного) государственного бюджета, и профицитная доля это:
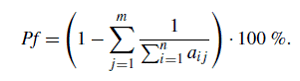 Поэтому государственный бюджет определяется на основе информации о значениях элементах в матрице взаимодействия А.
Поэтому государственный бюджет определяется на основе информации о значениях элементах в матрице взаимодействия А.
