В современном мире автомобиль перестал быть роскошью, он стал средством передвижения, доступным многим. Для большинства граждан предпочтительнее купить поддержанный автомобиль, а не новый, только что сошедший с конвейера. Какую сумму правильно будет заплатить за б/у автомобиль? За сколько можно продать свой автомобиль? С этими вопросами сталкиваются многие из нас. Чтобы правильно дать ответ, необходимо учесть определенные параметры: тип кузова, год выпуска, объем двигателя, тип коробки передач, пробег. Используя регрессионную модель в среде Gretl, можем найти зависимость стоимости автомобиля от данных параметров.
Ряд ученых изучает проблемы и методы построения различных регрессионных моделей. Базовые принципы использования метода регрессионного анализа были разработаны С.И. Носковым и М.П. Базилевским [1]. Использовалась множественная регрессия О.В. Гусевым и А.В. Жуковым [2] для идентификации перегрузки сервера. А.А. Жарков и Н.А. Анисимова [3] метод множественной регрессии применили для определения рыночной стоимости квартиры с учетом сроков и условий реализации жилья. Расчет логистических издержек при помощи метода множественной регрессии разработан И.А. Семеновым и А.А. Носковым [4]. С использованием Gretl определяются причины трудового оппортунизма сотрудников Р.З. Мухаметзяновым [5]. Особенности использования среды Gretl в целях построения экономических моделей рассматриваются А.А.Тусковым [6]. Особенности применения программных продуктов Excel и Gretl в рамках эконометрического моделирования рассмотрела Ю.Г.Зарезина [7]. Р.И. Баженовым и др. [8-14] изучены проблемы использования регрессионных моделей для анализов различных видов. Изучением регрессионного анализа занимаются также зарубежные ученые [15-16].
По данным сайта www.avito.ru был осуществлен сбор экспериментальных наблюдений. Рассматривались объявления о продаже автомобилей в г.Биробиджан и в г.Хабаровск. Были выбраны следующие критерии: марка, тип кузова, год выпуска, объем двигателя, тип коробки передач, тип привода, пробег, стоимость. 
Тип кузова кодируется следующим образом:
1 – седан;
2 – хэтчбэк;
3 – универсал;
4 – кроссовер;
5 – минивэн;
6 – пикап;
7 – внедорожник;
8 – купе.
Тип коробки передач обозначим:
1 – автоматическая;
2 – механическая.
Привод определим:
1 – передний;
2 – задний;
3 – полный.
Создадим таблицу данных в MS Excel. Используя данные 200 объявлений (рис.1).

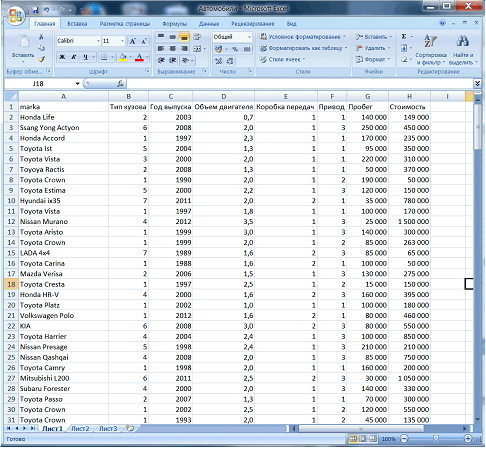
Введем обозначения переменных: тип кузова – х1, год выпуска – х2, объем двигателя – х3, коробка передач – х4, привод – х5, пробег – х6, стоимость – y (рис.2.). 

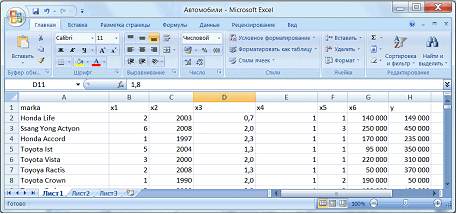
Рисунок 2 – Обозначение переменных

Следующий шаг – открыть данные таблицы Excel в Gretl (рис.3).

Рисунок 3 – Среда Gretl

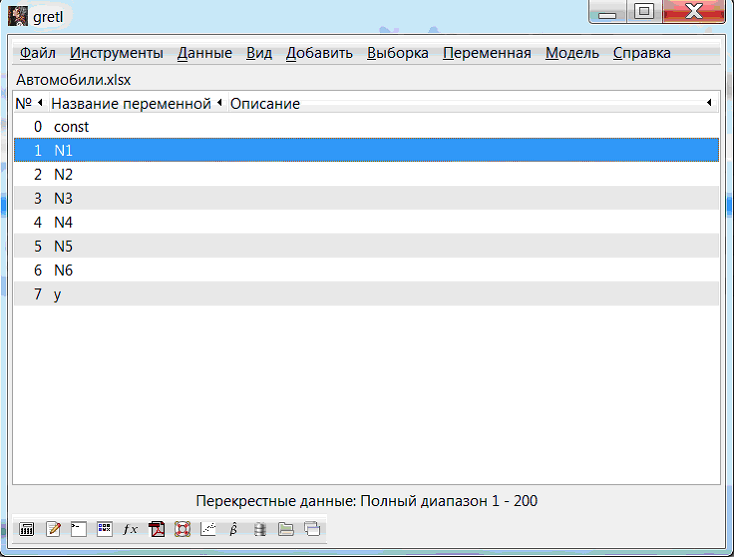
В окне программы появляются переменные, которые необходимы, чтобы построить регрессионную модель (рис.4).

Необходимо просмотреть получившуюся таблицу (рис. 5-6).

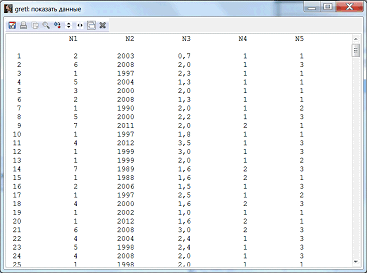
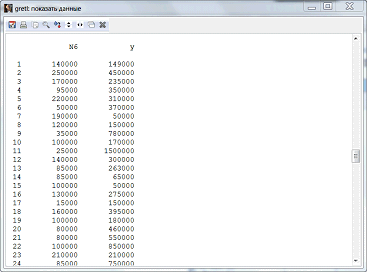
Так как у нас получилось больше шести столбцов данных, то оставшиеся 2 столбца найдем внизу таблицы (рис.7).

Для решения нашей задачи найдем регрессионную модель, используя метод наименьших квадратов (рис.8).

Перейдем к построению уравнения модели (рис.9) 

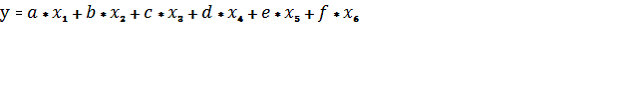
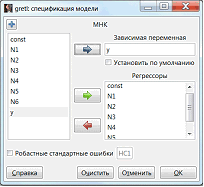
Рисунок 9 – Окно спецификации модели

Получившаяся модель и ее описательные статистики показаны на рисунке (рис.10).

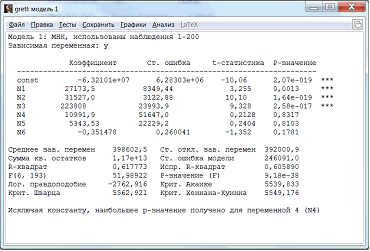
По значению R-квадрата можно судить о доле вариации результативного признака с учетом воздействия изучаемых факторов. В данной модели 61,8% вариации переменной Y зависит от влияния включенных факторов, 38,2% обусловлены другими факторами. Если коэффициент выше 80%, то модель считается достаточно хорошей. А у нас слишком низкий R-квадрат. Использование линейной аналитической формы модели может стать вероятной причиной ее слабости. Поэтому найдем другую модель. 
При помощи теста на нелинейность можно проверить обоснованность применения степенной модели (рис.11).

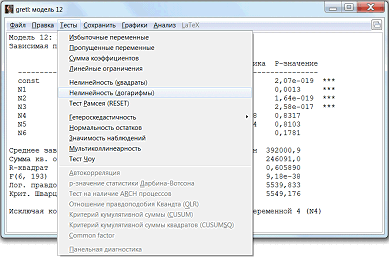
Рисунок 11 – Выбор теста на нелинейность

Проверим модель на нелинейность (логарифмы) (рис. 12).

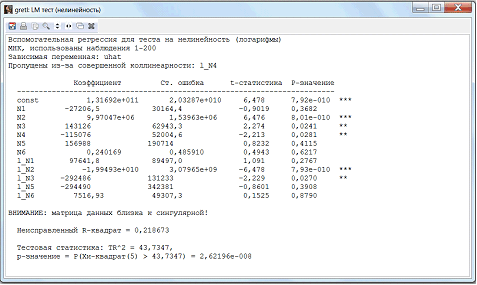
Тест нелинейности для логарифмов (значение p=0,0000001) свидетельствует, что нулевую гипотезу (о линейности аналитической формы) следует отклонить, поскольку значение TR² = 43,7347 превышает критическое значение х²(1%; 5) = 15,086; по этой причине существуют основания для принятия степенной формы модели (с логарифмированными переменными). 
Исследования параметров привели к выводу, что существует логарифмическая зависимость.
Найдем зависимость lny от х₁, х₂, х₃, х₄, х₅, lnx₆ (рис.13).

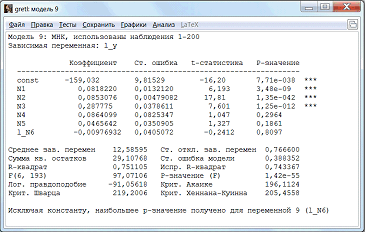
Рисунок 13 – Новая регрессионная модель

В этой модели R-квадрат у нас уже 75,1%. Значит, модель более точная, чем предыдущая.
Перейдем к решению уравнения

Введем в Excel данные const, х₁, х₂, х₃, х₄, х₅, х₆ (рис. 14). Коэффициенты: a – тип кузова, b – год выпуска, с – объем двигателя, d – коробка передач, e – привод, f – пробег. 

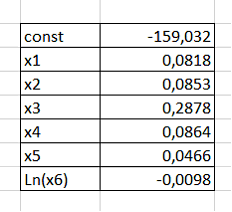
Рисунок 14 – Данные в Excel

В ячейку, окрашенную в оранжевый цвет, вводим формулу расчета (рис.15). В таблицу Excel вводим необходимые параметры того автомобиля, который мы хотим купить или продать, в ячейки, окрашенные в синий цвет.

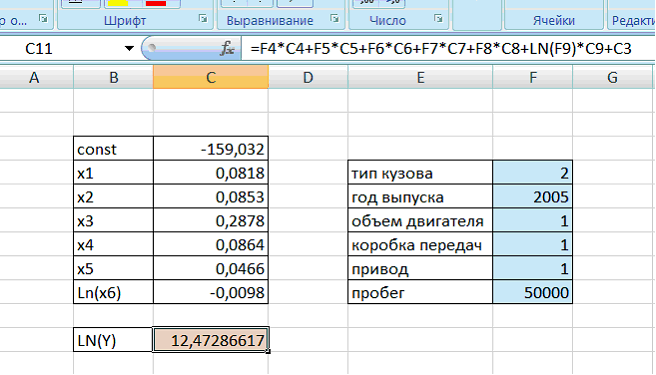
Рисунок 15 – Ввод данных

В ячейку, окрашенную в зеленый цвет, вводим формулу расчета стоимости автомобиля. После этого в ячейке, выделенной зеленым цветом, отобразится стоимость данного автомобиля (рис.16).

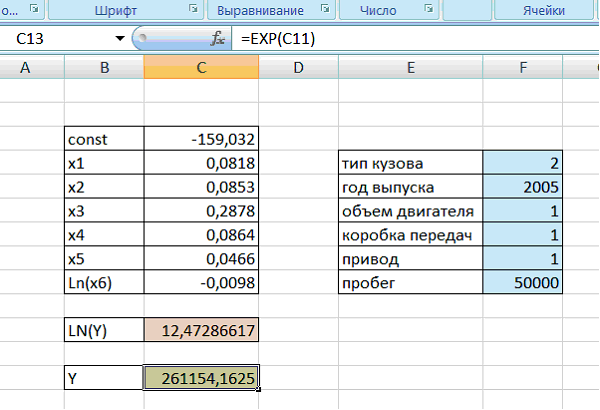
Рисунок 16 – Расчет стоимости автомобиля по заданным параметрам

Если мы хотим узнать стоимость другого автомобиля, то нужно просто в ячейки, окрашенные в синий цвет ввести другие параметры.
Полученную регрессионную модель можно использовать в работе агентств, занимающихся продажей поддержанных автомобилей. Описание принципов построения регрессионной модели может пригодиться в преподавании студентам различных направлений [17-19].

1. Базилевский М.П., Носков С.И. Методические и инструментальные средства построения некоторых типов регрессионных моделей // Системы. Методы. Технологии. 2012. №1. С. 80-87.
2. Гусев О.В., Жуков А.В. Способ идентификации перегрузки с использованием множественной регрессии // Информационная среда вуза XXI века. Материалы VII Международной научно-практической конференции. Петрозаводск, 2013. С. 57-61.
3. Жарков А.А., Анисимова Н.А. Механизм формирования стоимости квартир на региональном рынке жилья // Регион: системы, экономика, управление. 2009. № 4. С. 47-53.
4. Семенов И.А., Носков А.А. Модель расчета общих логистических издержек методом множественной регрессии // Вестник Саратовского государственного технического университета. 2011. Т. 4. № 2с. С. 397-400.
5. Мухаметзянов Р.З. Анализ трудового оппортунизма сотрудников // Science time. 2014. №6 (6). С. 132-147.
6. Тусков А.А. Применение Gretl для построения многофакторной модели // Модели, системы, сети в экономике, технике, природе и обществе. 2011. №1. С. 154-159.
7. Зарезина Ю.Г. Особенности применения программных продуктов Excel и Gretl в рамках эконометрического моделирования // Новое слово в науке и практике: гипотезы и апробация результатов исследований. 2015. № 15. С. 223-228.
8. Пронина О.Ю., Баженов Р.И. Исследование методов регрессионного анализа программной среды Eviews // Nauka-Rastudent.ru. 2015. № 1 (13). С. 45.
9. Лагунова А.А., Баженов Р.И. Разработка в среде Gretl регрессионной модели рынка вторичного жилья г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 40.
10. Муллинов Д.О., Баженов Р.И. Разработка в среде Eviews регрессионной модели рынка гаражных помещений г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 43.
11. Баженов Р.И. Информационная безопасность и защита информации: практикум. Биробиджан: Изд-во ГОУВПО «ДВГСГА», 2011. 140 с.
12. Vexler V.A., Bazhenov R.I., Bazhenova N.G. Entity-relationship model of adult education in regional extended education system // Asian Social Science. 2014. Т. 10. № 20. С. 1-14.
13. Векслер В.А., Баженов Р.И. Формирование модели обучения взрослых основам информационных технологий: региональный аспект: монография. -Биробиджан: Издательский центр ФГБОУ ВПО «ПГУ им. Шолом-Алейхема», 2014. 126 с.
14. Наумов А.А., Баженов Р.И. О неустойчивости метода нормализации критериев // Современные научные исследования и инновации. 2014. № 11-1 (43). С. 64-68.
15. Baiocchi G., Distaso W. GRETL: Econometric software for the GNU generation // Journal of Applied Econometrics.  2003.  Т. 18.  №. 1.  С. 105-110.
16. Mixon Jr J. W., Smith R. J. Teaching undergraduate econometrics with GRETL // Journal of Applied Econometrics.  2006.  Т. 21.  №. 7.  С. 1103-1107.
17. Баженов Р.И. Об организации научно-исследовательской практики магистрантов направления «Информационные системы и технологии» // Современные научные исследования и инновации. 2014. № 9-2 (41). С. 62-69.
18. Баженов Р.И. Проектирование методики обучения дисциплины «Интеллектуальные системы и технологии» // Современные научные исследования и инновации. 2014. № 5-2 (37). С. 48.
19. Баженов Р.И. Об организации деловых игр в курсе «Управление проектами информационных систем» // Научный аспект. 2014. Т. 1. № 1. С. 101-102.

Все статьи автора «Баженов Руслан Иванович»