Актуальность вопросов, связанных с обоснованием применения того или иного метода учёта неопределенности при экономической оценке инвестиций, вытекает из следующих положений. Во-первых, в современных нестабильных условиях, несомненно, необходимо формализовать подход к выявлению и ограничению многочисленные неопределённостей, которые влияют на все без исключения строительные предприятия. Во-вторых, процедура технико-экономического обоснования ИСП предполагает определенную степень прогнозирования, т. е. решения часто принимаются на основе прошлого опыта (либо рационально, либо интуитивно), с некоторой степенью неопределенности. Следовательно, первостепенной важностью для строительной организации является умение предсказывать и сравнивать все возможные будущие денежные результаты с учетом неотъемлемой неопределенности, связанной с выбранным параметрам инвестиций, включая затраты на строительство, эксплуатацию и техническое обслуживание, процентные ставки, инфляцию, амортизацию, ставку налога и срок эксплуатации [1].
Автором в работе [2] была рассчитана эффективность конкретного инвестиционно-строительного проекта (ИСП) методом определения чистой текущей стоимости (ЧДД, NPV). Оценка эффективности основана на данных «Cash Flow» и процедуре дисконтирования денежных потоков, приведенных их к настоящему моменту времени. Планирование выполнялось с использованием компьютерной модели Excel 2003. На основании представленных сведений были проделаны расчеты финансово-экономической модели реализации проекта. Далее было проведено его экономическое обоснование и оценка эффективности.
На основании расчетов показателей эффективности получены следующие данные: накопленный чистый дисконтированный денежный поток до 2025 года составляет 277403 тыс. руб.; внутренняя норма доходности – 56,71%; срок окупаемости – 3,7 года (см. график 1 и 2), с учетом дисконтирования – 3,9 года; коэффициент рентабельности инвестированного капитала составляет 17,53%; модифицированная внутренняя норма рентабельности – 25,9%. Проведенный экономический анализ показал, что каждый вложенный в проект рубль окупит себя и принесет дополнительно 7,13 рубля.

График 1 – Финансовый профиль проекта, тыс. руб.
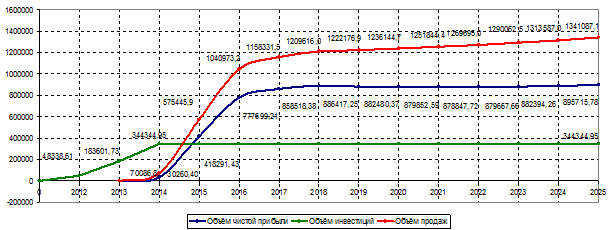
График 2 – Карта рентабельности проекта, тыс. руб. [3]
Резюмируя, отметим, что проект является финансово реализуемым, целесообразным и будет востребован среди потенциальных покупателей объектов жилищной недвижимости в Москве, поскольку данный сегмент имеет платежеспособный спрос на анализируемый объект. Полученные результаты анализа указывают на экономическую целесообразность инициации данного проекта, однако они не учитывают всех факторов, а именно, факторов неопределённости и риска. В связи с этим, для комплексной оценки эффективности ИСП нам необходимо совершить оценку его неопределённостей и выяснить эффективность проекта с их учётом. Следовательно, перед нами встаёт задача построения экономико-математической модели ИСП в стохастических условиях. Для её решения будем поочерёдно применять различные инструменты анализа рисков и анализировать полученные результаты.
1. Метод безрискового эквивалента (метод риск-нейтрального денежного потока). Чистый дисконтированный доход от реализации проекта соответствует расчётам, проведённым в таблице 1. Необходимо рассчитать эффективность проекта с учетом того, что по результатам экспертных оценок были получены величины коэффициентов достоверности, а ставка по безрисковой доходности равна 8%.
Таблица 1 – Расчет скорректированного потока платежей
|
t |
1/(1+0,08)t |
CFt |
at |
at*CFt |
PV=гр.5*гр.2 |
|
|
2012 |
1 |
0,9259259 |
-48592,9 |
1,2 |
-58311,5 |
-53992,1352 |
|
2013 |
2 |
0,8573388 |
-139672 |
1,5 |
-209509 |
-179619,91 |
|
2014 |
3 |
0,7938322 |
-113343 |
1,3 |
-147345 |
-116967,416 |
|
2015 |
4 |
0,7350299 |
428581,4 |
0,9 |
385723,2 |
283518,0974 |
|
2016 |
5 |
0,6805832 |
365314,8 |
0,82 |
299558,1 |
203874,2394 |
|
2017 |
6 |
0,6301696 |
86726,19 |
0,61 |
52902,98 |
33337,84874 |
|
2018 |
7 |
0,5834904 |
33805,89 |
0,53 |
17917,12 |
10454,46968 |
|
2019 |
8 |
0,5402689 |
1970,148 |
0,45 |
886,5668 |
478,9844349 |
|
2020 |
9 |
0,500249 |
3279,251 |
0,38 |
1246,115 |
623,3679515 |
|
2021 |
10 |
0,4631935 |
4902,147 |
0,32 |
1568,687 |
726,6056082 |
|
2022 |
11 |
0,4288829 |
6726,968 |
0,29 |
1950,821 |
836,673611 |
|
2023 |
12 |
0,3971138 |
8633,63 |
0,26 |
2244,744 |
891,4186542 |
|
2024 |
13 |
0,3676979 |
11041,78 |
0,21 |
2318,773 |
852,607976 |
|
2025 |
14 |
0,340461 |
14093,79 |
0,19 |
2677,82 |
911,6933956 |
|
NPV |
277402,8 |
185926,546 |
На конкретном примере показано, что чистая текущая стоимость потока платежей, скорректированного с учетом риска, составляет 185 926,55 тыс. руб., что на 32,96% меньше исходной величины.
2. Метод построения сценариев. Отдельного внимания заслуживает анализ чувствительности проекта, по результатам которого, были составлены три сценария развития ИСП и установлены вероятности их реализации (табл. 2). Проведём исследование собственного риска проекта при условии, что все другие величины считаются детерминированными. С целью минимизации вычислений эти значения показаны в таблице 2.
Таблица 2 – Сценарии реализации инвестиционно-строительного проекта
| Сценарий Показатели |
Наихудший |
Наилучший |
Вероятный |
| Объём реализации жилых площадей, м2 – Qж |
6893,75 |
10289,18 |
8951,59 |
| Объём реализации машиномест в паркинге, м2 – Qм |
128 |
152 |
141 |
| Цена за 1 кв.м. реализуемых жилых площадей, руб./м2 – Pж |
111,43 |
160,41 |
122,45 |
| Цена за 1 машино-места, тыс.руб. – Pм |
1131 |
1573 |
1300 |
| Переменные затраты, тыс. руб. – V |
67357,33 |
38567,51 |
54320,43 |
| Ставка дисконтирования, % – r |
20,56 |
10,17 |
14,19 |
| Инвестиционные затарты, тыс. руб. – IC |
430431,19 |
258258,72 |
344344,95 |
| NPV, тыс. руб. |
158691,26 |
317501,81 |
223508,81 |
Рассчитанные выше данные указывают на то, что дисперсия (разброс) потенциальных результатов достаточно велика. Найдем среднее ожидаемое значение NPV – величину Е (NPV) = 158691,26*0,27+317501,81*0,31+ 223508,81*0,42 = 235145,903. Далее вычислим стандартное отклонение NPV, воспользовавшись соотношением:  79850,6838 (рассчитано в Excel 2003). Исследование также показало, что с вероятностью 68% можно утверждать, что NPV проекта будет располагаться в диапазоне 235145,903 ± 79850,6838 (от 155295,219 до 314996,59). Следовательно, вероятность отклонения от ожидаемого NPV в меньшую или большую сторону на величину
79850,6838 (рассчитано в Excel 2003). Исследование также показало, что с вероятностью 68% можно утверждать, что NPV проекта будет располагаться в диапазоне 235145,903 ± 79850,6838 (от 155295,219 до 314996,59). Следовательно, вероятность отклонения от ожидаемого NPV в меньшую или большую сторону на величину  будет равна приблизительно 34%. Ниже представлена таблица с итогами вероятностного анализа для рассматриваемого проекта.
будет равна приблизительно 34%. Ниже представлена таблица с итогами вероятностного анализа для рассматриваемого проекта.
Таблица 3 – Результаты вероятностного анализа по функции Лапласа
|
NPV, тыс. руб. |
|||
| Среднее |
233233,96 |
Минимум |
158691,26 |
| Стандартная ошибка |
46101,814 |
Максимум |
317501,81 |
| Медиана |
223508,81 |
Сумма |
699701,88 |
| Стандартное отклонение |
79850,684 |
Счет |
3 |
| Коэффициент вариации |
2,9208762 |
вероятность p(NPV=0) |
0,17% |
| Дисперсия выборки |
6,38E+09 |
вероятность p(NPV<=среднее) |
50,00% |
| Асимметричность |
0,5399329 |
вероятность p(NPV<=максисум) |
85,44% |
| Интервал |
158810,55 |
Уровень надежности(95,0%) |
198360,1 |
Применение обозначенного метода было направлено на анализ поведения величины NPV. Полученные результаты, в общем, подтверждают гипотезу об отсутствии риска касательно рассматриваемого ИСП. Исследование показало, что средняя величина NPV (235145,903) существенно превосходит экспертный прогноз (3658,73); величина этого показателя значительно выше стандартного отклонения (79850,6838), что указывает на финансовую устойчивость проекта к риску. Вероятность получения нулевого результата равна 0,17%, следовательно, имеется один “шанс” из 588, что строительная компания понесет убытки, реализовав данный проект.
3. Метод корректировки ставки дисконтирования с учетом риска (risk adjusted discount rate approach). Для осуществления сравнительного анализа будем корректировать ставку дисконтирования, включив в её состав показатель вероятности риска.
Модель 1. Расчёт по уровню ставки рефинансирования и уровню инфляции. Вначале установим ставку дисконтирования с поправкой на риск по формуле:  , где n1 – реальная ставка ссудного процента; n2 – темп инфляции; n3 – вероятность риска. Находим переменные: примем ставку рефинансирования на уровне 8,00%, темп инфляции на уровне 6,5%, тогда n1 – 8%; n2 – согласно официальному прогнозу Минэкономразвития, инфляция в 2012 году составит 6,5%; n3 – 4% (для данного ИСП аналитиками СУ-155 вероятность риска оценивается в 4%), тогда:
, где n1 – реальная ставка ссудного процента; n2 – темп инфляции; n3 – вероятность риска. Находим переменные: примем ставку рефинансирования на уровне 8,00%, темп инфляции на уровне 6,5%, тогда n1 – 8%; n2 – согласно официальному прогнозу Минэкономразвития, инфляция в 2012 году составит 6,5%; n3 – 4% (для данного ИСП аналитиками СУ-155 вероятность риска оценивается в 4%), тогда:  . В соответствии с полученной ставкой в 19,62% рассчитываем чистую приведённую стоимость: NPV = 199 385,02 тыс. руб. Дополнительно найдём внутреннюю норму доходности и другие финансово-экономические показатели проекта согласно изменённым дисконтированным доходом: IRR = 56,71%; ROIC =12,6%; MIRR = 26,41%; PI =1,87.
. В соответствии с полученной ставкой в 19,62% рассчитываем чистую приведённую стоимость: NPV = 199 385,02 тыс. руб. Дополнительно найдём внутреннюю норму доходности и другие финансово-экономические показатели проекта согласно изменённым дисконтированным доходом: IRR = 56,71%; ROIC =12,6%; MIRR = 26,41%; PI =1,87.
Модель 2. Средневзвешенная стоимость капитала (weighted average cost of capital — WACC), которая учитывает стоимость собственного (акционерного) капитала и стоимость заемных средств: WACC= Re(E/V) + Rd(D/V)(1 — tc), где Re — ставка доходости собственного (акционерного) капитала, рассчитанная с использованием модели capital assets pricing model – CAPM по формуле Re = Rf + β(Rm — Rf). Рассчитаем новую ставку дисконтирования с учётом риска: средневзвешенная стоимость капитала WACC=20,1%*0,27+12%*0,73=14,19%. Рассчитаем новое значение чистого дисконтированного дохода и другие финансово-экономические показатели проект: NPV = 277 403, 81 тыс. руб., IRR = 56,71%; ROIC =17,53%; MIRR = 25,9%; ROI = 7,13
Модель 3. Кумулятивный метод оценки ставки дисконтирования определяется исходя из следующей формулы: d = Emin + I + r, где d – ставка дисконтирования (номинальная); Emin — минимальная реальная ставка дисконтирования; I — темп инфляции; r — коэффициент, учитывающий уровень инвестиционного риска (премия за риск). Применительно к рассматриваемому проекту d = 8% + 6,5 + 4%=18,5% и NPV = 213 536,18 тыс. руб.; ROIC = 13,49%; MIRR = 26,31%; PI = 1,87. Произведём сравнительный анализ показателей, определённых с учётом риска (табл. 4).
Таблица 4 – Сравнительный анализ показателей эффективности ИСП с учётом рисков
|
Показатель |
Модель1 d=19,62% |
Модель2 d=14,18% |
Модель3 d=18,5% |
|
NPV |
277 402,81 |
213 536,18 |
199 385,02 |
|
PI |
2,09 |
1,91 |
1,87 |
|
ROIC |
17,53% |
13,49% |
12,60% |
|
MIRR |
25,90% |
26,31% |
26,41% |
|
DPB |
3,9 |
3,96 |
3,98 |
Оценивая ИСП, отметим, что при корректировке ставки дисконтирования получаемые показатели оценки эффективности проекта колеблются не сильно. Их расчётные значения соблюдают требования эффективности (прибыльности) инвестиционного проекта, а именно: NPV > 0; PI > 1; IRR>E и др.
4. Имитационное моделирование рисков методом Монте-Карло (Monte-Carlo Simulation). Автоматическое решение задачи предполагает использование средства Excel «Диспетчер сценариев». Границы наиболее вероятных колебаний исходных показателей определены в таблице 5.
Таблица 5 – Исходные условия эксперимента
|
минимум |
максимум |
||||||||
|
Инвестиционная деятельность |
258258,716 |
430431,193 |
|||||||
|
Переменные затраты – V, тыс. руб. |
1248,71547 |
6243,57737 |
|||||||
|
Цена – Р, тыс. руб. |
1-комнатные квартиры |
100 |
160 |
||||||
|
2-комнатные квартиры |
90 |
150 |
|||||||
|
3-комнатные квартиры |
80 |
140 |
|||||||
|
4-комнатные квартиры |
70 |
130 |
|||||||
|
машиноместа в паркинге |
1000 |
1600 |
|||||||
|
коммерческие (офисные) площади |
3 |
4 |
|||||||
|
Объем выпуска – Q, шт. |
1-комнатные квартиры |
7 |
14 |
30 |
70 |
15 |
45 |
- |
- |
|
2-комнатные квартиры |
5 |
12 |
35 |
75 |
15 |
45 |
- |
- |
|
|
3-комнатные квартиры |
2 |
6 |
15 |
50 |
35 |
65 |
- |
- |
|
|
4-комнатные квартиры |
0 |
4 |
10 |
40 |
40 |
80 |
- |
- |
|
|
машиноместа в паркинге |
0 |
2 |
9 |
25 |
24 |
45 |
15 |
40 |
|
|
коммерческие (офисные) площади |
- |
- |
50 |
100 |
100 |
100 |
100 |
100 |
|
|
минимум |
максимум |
мин |
макс |
мин |
мак |
мин |
макс |
||
|
Год реализации проекта |
2014 |
2015 |
2016 |
2017 |
|||||
Основное содержание исследования составляют результаты имитационного моделирования ИСП, которые приведены в таблице 6.
Таблица 6 – Имитационный анализ (Метод Монте-Карло)
|
количество |
цена |
||||||||||
| показатели |
перем. расходы |
2014 |
2015 |
2016 |
2017 |
1-к |
2-к |
3-к |
4-к |
Маш. |
Ком. |
| среднее значение |
271756,6 |
26,77 |
164,39 |
170,47 |
38,37 |
128,60 |
119,14 |
108,11 |
101,5 |
1290,3 |
3,94 |
| станд. Отклон. |
1352,932 |
12,99 |
8,92 |
7,43 |
15,85 |
16,612 |
17,227 |
17,652 |
18,12 |
171,99 |
0,578 |
| коэф. Вариации |
0,004978 |
0,485 |
0,0543 |
0,0436 |
0,413 |
0,1291 |
0,1445 |
0,163 |
0,178 |
0,1332 |
0,1470 |
| минимум |
269459,7 |
100,04 |
90,28 |
80,05 |
70,00 |
1010,04 |
3,03 |
||||
| максимум |
274337,72 |
160,06 |
148,17 |
140,47 |
130,55 |
1591,11 |
4,98 |
||||
| вероятность p(NPV<=X) |
вел Х |
нормал Х |
250000 |
p(NPV<=X) |
0,0783 |
||||||
Сопоставим полученные показатели с данными анализа, проведенного в соответствии со сценарным анализом. По данным имитационного моделирования риск проекта немного больше. Уровень NPV ниже результата предшествующего исследования (232285,24 и 233233,96 соответственно). Тем не менее, размер стандартного отклонения также значительно меньше (79850,684 и 28228,9) и не превосходит NPV. Коэффициент вариации (0,122) ниже 1, следовательно, риск анализируемого ИСП в общей сложности меньше среднего риска инвестиционного портфеля фирмы. Итоги вероятностного анализа свидетельствуют, что “шанс” получить отрицательную величину NPV не превышает 0,2%.
5. Методы теории игр – Theory of Games (критерий максимакса, Вальда, Сэвиджа, Гурвица и Байеса-Лапласа). Найдем стратегии решений в условиях риска при помощи методов теории «игр с природой». В изображенных матрицах столбцы отвечают конкретным состояниям внешней среды Sj (величина спроса на жилплощадь), а элементы aij по строкам – состояния «природы» интерпретируем как сценарии будущего, которым отвечают NPV для каждого инвестиционного варианта.
Допустим, имеется 10 вариантов инвестирования – С1, С2, С3, С4, С5, С6,С7,С8,С9 и С10. По каждому из них равновероятны 4 ситуации – консервативная, оптимистическая, пессимистическая и смешанная. Для вычисления вероятностных характеристик риска ниже составлены матрицы доходности и матрица рисков (для критерия Севиджа). Для избрания лучшей стратегии инвестирования нам целесообразно рассчитать несколько критериев, а именно, Сэвиджа, Вальда, Гурвица и Байеса. Коэффициент пессимизма равен 0,6. Примем, что вероятность наступления оптимистического сценария – 0,2, пессимистического – 0,2, смешанного – 0,1, консервативного – 0,5. Расчёты представлены в таблицах 7-10.
Таблица 7 – Расчет вероятностных критериев риска по методу Вальда
|
критерий Вальда |
Состояние внешней среды (величина спроса на жилплощадь (м2) и маш./места (шт.) в течение 2014-2017 гг. |
||||
|
Стратегия (цена реализации 1м2 и 1 маш./места) |
Оптимистич. сценарий S1 (11682м2 и 152 шт.) |
Консервативый сценарий S2 (135 10289м2 и шт.) |
Пессимистич. сценарий S3 (8567м2 и 95 шт.) |
Смешанный сценарий S4 (9513м2 и 128 шт.) |
min aij |
|
Ц (1м2)=115,58тыс. руб.; Ц (1м/м)=1038,88тыс. руб. |
262500,11 |
218750,09 |
185937,58 |
222395,92 |
185937,58 |
|
Ц (1м2)=131,83тыс. руб.; Ц (1м/м)=1180,58тыс. руб. |
306145,04 |
255120,8628 |
216852,73 |
259372,88 |
216852,73 |
|
Ц (1м2)=119,44тыс. руб.; Ц (1м/м)=1227,59тыс. руб. |
273650,78 |
228042,3201 |
193835,97 |
231843,03 |
193835,97 |
|
Ц (1м2)=118,01тыс. руб.; Ц (1м/м)=1322,26тыс. руб. |
267262,03 |
222718,3546 |
189310,60 |
226430,33 |
189310,60 |
| Ц (1м2)=95,91тыс. руб.; Ц (1м/м)=1375,03тыс. руб. |
207305,54 |
172754,6169 |
146841,42 |
175633,86 |
146841,42 |
|
Ц (1м2)=108,13тыс. руб.; Ц (1м/м)=1096,33тыс. руб. |
228097,57 |
190081,3056 |
161569,11 |
193249,33 |
161569,11 |
|
Ц (1м2)=115,07тыс. руб.; Ц (1м/м)=1103,51тыс. руб. |
264274,03 |
220228,3562 |
187194,10 |
223898,83 |
187194,10 |
|
Ц (1м2)=111,15тыс. руб.; Ц (1м/м)=1396,36тыс. руб. |
313060,91 |
260884,0883 |
221751,48 |
265232,16 |
221751,48 |
|
Ц (1м2)=131,67тыс. руб.; Ц (1м/м)=1597,83тыс. руб. |
292065,59 |
243387,991 |
206879,79 |
247444,46 |
206879,79 |
|
Ц (1м2)=122,97тыс. руб.; Ц (1м/м)=1474,12тыс. руб. |
282854,77 |
235712,3101 |
200355,46 |
239640,85 |
200355,46 |
|
max min aij |
221751,48 |
||||
Таблица 8 – Расчет вероятностных критериев риска по методу Севиджа
|
критерий Севиджа критерий Абсолютного оптимизма |
Состояние внешней среды (величина спроса на жилплощадь (м2) и маш./места (шт.) в течение 2014-2017 гг. |
||||
|
Стратегия (цена реализации 1м2 и 1 маш./места) |
Оптимистич. сценарий S1 (11682м2 и 152 шт.) |
Консервативый сценарий S2 (135 10289м2 и шт.) |
Пессимистич. сценарий S3 (8567м2 и 95 шт.) |
Смешанный сценарий S4 (9513м2 и 128 шт.) |
mах aij |
|
Ц (1м2)=115,58тыс. руб.; Ц (1м/м)=1038,88тыс. руб. |
262500,11 |
218750,09 |
185937,58 |
222395,92 |
262500,11 |
|
Ц (1м2)=131,83тыс. руб.; Ц (1м/м)=1180,58тыс. руб. |
306145,04 |
255120,86 |
216852,73 |
259372,88 |
306145,04 |
|
Ц (1м2)=119,44тыс. руб.; Ц (1м/м)=1227,59тыс. руб. |
273650,78 |
228042,32 |
193835,97 |
231843,03 |
273650,78 |
|
Ц (1м2)=118,01тыс. руб.; Ц (1м/м)=1322,26тыс. руб. |
267262,03 |
222718,35 |
189310,60 |
226430,33 |
267262,03 |
|
Ц (1м2)=95,91тыс. руб.; Ц (1м/м)=1375,03тыс. руб. |
207305,54 |
172754,62 |
146841,42 |
175633,86 |
207305,54 |
|
Ц (1м2)=108,13тыс. руб.; Ц (1м/м)=1096,33тыс. руб. |
228097,57 |
190081,31 |
161569,11 |
193249,33 |
228097,57 |
|
Ц (1м2)=115,07тыс. руб.; Ц (1м/м)=1103,51тыс. руб. |
264274,03 |
220228,36 |
187194,10 |
223898,83 |
264274,03 |
|
Ц (1м2)=111,15тыс. руб.; Ц (1м/м)=1396,36тыс. руб. |
313060,91 |
260884,09 |
221751,48 |
265232,16 |
313060,91 |
|
Ц (1м2)=131,67тыс. руб.; Ц (1м/м)=1597,83тыс. руб. |
292065,59 |
243387,99 |
206879,79 |
247444,46 |
292065,59 |
|
Ц (1м2)=122,97тыс. руб.; Ц (1м/м)=1474,12тыс. руб. |
282854,77 |
235712,31 |
200355,46 |
239640,85 |
282854,77 |
|
min max rij |
|
|
|
|
207305,54 |
|
max max aij |
313060,91 |
||||
Таблица 9 – Расчет вероятностных критериев риска по методу Гурвица
|
критерий Гурвица |
Состояние внешней среды (величина спроса на жилплощадь (м2) и маш./места (шт.) в течение 2014-2017 гг. |
||||||
|
Стратегия (цена реализации 1м2 и 1 маш./места) |
Оптимистич. сценарий S1 (11682м2 и 152 шт.) |
Консервативый сценарий S2 (135 10289м2 и шт.) |
Пессимистич. сценарий S3 (8567м2 и 95 шт.) |
Смешанный сценарий S4 (9513м2 и 128 шт.) |
max aij |
min aij |
αmax aij +βmin aij, при α=0,7 и β=0,3 |
|
Ц (1м2)=115,58тыс. руб.; Ц (1м/м)=1038,88тыс. руб. |
262500,11 |
218750,09 |
185937,58 |
222395,92 |
262500,11 |
185937,58 |
239531,35 |
|
Ц (1м2)=131,83тыс. руб.; Ц (1м/м)=1180,58тыс. руб. |
306145,04 |
255120,86 |
216852,73 |
259372,88 |
306145,04 |
216852,73 |
279357,34 |
|
Ц (1м2)=119,44тыс. руб.; Ц (1м/м)=1227,59тыс. руб. |
273650,78 |
228042,32 |
193835,97 |
231843,03 |
273650,78 |
193835,97 |
249706,34 |
|
Ц (1м2)=118,01тыс. руб.; Ц (1м/м)=1322,26тыс. руб. |
267262,03 |
222718,35 |
189310,60 |
226430,33 |
267262,03 |
189310,60 |
243876,60 |
|
Ц (1м2)=95,91тыс. руб.; Ц (1м/м)=1375,03тыс. руб. |
207305,54 |
172754,62 |
146841,42 |
175633,86 |
207305,54 |
146841,42 |
189166,31 |
|
Ц (1м2)=108,13тыс. руб.; Ц (1м/м)=1096,33тыс. руб. |
228097,57 |
190081,31 |
161569,11 |
193249,33 |
228097,57 |
161569,11 |
208139,03 |
|
Ц (1м2)=115,07тыс. руб.; Ц (1м/м)=1103,51тыс. руб. |
264274,03 |
220228,36 |
187194,10 |
223898,83 |
264274,03 |
187194,10 |
241150,05 |
|
Ц (1м2)=111,15тыс. руб.; Ц (1м/м)=1396,36тыс. руб. |
313060,91 |
260884,09 |
221751,48 |
265232,16 |
313060,91 |
221751,48 |
285668,08 |
|
Ц (1м2)=131,67тыс. руб.; Ц (1м/м)=1597,83тыс. руб. |
292065,59 |
243387,99 |
206879,79 |
247444,46 |
292065,59 |
206879,79 |
266509,85 |
|
Ц (1м2)=122,97тыс. руб.; Ц (1м/м)=1474,12тыс. руб. |
282854,77 |
235712,31 |
200355,46 |
239640,85 |
282854,77 |
200355,46 |
258104,98 |
|
max aij |
285668,08 |
||||||
Таблица 10 – Расчет вероятностных критериев риска по методу Лапласа
|
критерий Лапласа |
Состояние внешней среды (величина спроса на жилплощадь (м2) и маш./места (шт.) в течение 2014-2017 гг. |
||||
|
Стратегия (цена реализации 1м2 и 1 маш./места) |
Оптимистич. сценарий S1 (11682м2 и 152 шт.) |
Консервативый сценарий S2 (135 10289м2 и шт.) |
Пессимистич. сценарий S3 (8567м2 и 95 шт.) |
Смешанный сценарий S4 (9513м2 и 128 шт.) |
max ∑Pi*aij |
|
Ц (1м2)=115,58тыс. руб.; Ц (1м/м)=1038,88тыс. руб. |
262500,11 |
218750,09 |
185937,58 |
222395,92 |
221302,17 |
|
Ц (1м2)=131,83тыс. руб.; Ц (1м/м)=1180,58тыс. руб. |
306145,04 |
255120,86 |
216852,73 |
259372,88 |
258097,27 |
|
Ц (1м2)=119,44тыс. руб.; Ц (1м/м)=1227,59тыс. руб. |
273650,78 |
228042,32 |
193835,97 |
231843,03 |
230702,81 |
|
Ц (1м2)=118,01тыс. руб.; Ц (1м/м)=1322,26тыс. руб. |
267262,03 |
222718,35 |
189310,60 |
226430,33 |
225316,74 |
|
Ц (1м2)=95,91тыс. руб.; Ц (1м/м)=1375,03тыс. руб. |
207305,54 |
172754,62 |
146841,42 |
175633,86 |
174770,09 |
|
Ц (1м2)=108,13тыс. руб.; Ц (1м/м)=1096,33тыс. руб. |
228097,57 |
190081,31 |
161569,11 |
193249,33 |
192298,92 |
|
Ц (1м2)=115,07тыс. руб.; Ц (1м/м)=1103,51тыс. руб. |
264274,03 |
220228,36 |
187194,10 |
223898,83 |
222797,69 |
|
Ц (1м2)=111,15тыс. руб.; Ц (1м/м)=1396,36тыс. руб. |
313060,91 |
260884,09 |
221751,48 |
265232,16 |
263927,74 |
|
Ц (1м2)=131,67тыс. руб.; Ц (1м/м)=1597,83тыс. руб. |
292065,59 |
243387,99 |
206879,79 |
247444,46 |
246227,52 |
|
Ц (1м2)=122,97тыс. руб.; Ц (1м/м)=1474,12тыс. руб. |
282854,77 |
235712,31 |
200355,46 |
239640,85 |
238462,29 |
|
вероятность, Р |
0,20 |
0,50 |
0,20 |
0,10 |
|
|
max max aij |
|
|
|
|
263927,74 |
Раскроем содержательно полученные результаты. По критерию Вальда оптимальной из наихудших показателей имеет альтернатива С8, для неё а3=221751,48 тыс. руб. Согласно критерию максимального оптимизма, для приведенного примера из наибольших значений показателя наименьшим является величина а1=313060,91 тыс. руб., поэтому выбираем альтернативу С8. В соответствии с критерием Сэвиджа, самый маленький риск равен а1=207305,541 тыс. руб. Получаем альтернативу С5 с наименьшей функцией полезности. По критерию Гурвица предпочтительной является стратегия С8 = 285668,08 тыс. руб. Основываясь на критерии Лапласа, функция полезности предельна для альтернативы С8 = 263927,74 тыс. руб., следовательно, ее рациональнее всего принять. Рассчитав значения элементов матрицы NPV с использованием критериев максимакса, Вальда, Сэвиджа, Гурвица и Байеса-Лапласа, мы получили, что оптимальным вариантом реализации проекта является стратегия С8 (Ц (1м2)=111,15тыс. руб.; Ц (1м/м)=1396,36тыс. руб.).
6. Метод оценки риска неэффективности инвестирования на основе теории нечетких множеств. Взяв за наиболее ожидаемую ставку дисконтирования величину  , мы нашли наиболее ожидаемую величину чистой приведенной стоимости
, мы нашли наиболее ожидаемую величину чистой приведенной стоимости  тыс. руб. (по результатам имитационного моделирования Монте-Карло). Минимально возможное значение
тыс. руб. (по результатам имитационного моделирования Монте-Карло). Минимально возможное значение  составляет 183838 тыс. руб., а максимально возможное значение
составляет 183838 тыс. руб., а максимально возможное значение  – это прибыль в 301184 тыс. руб. Установленное предприятием условие – это то, чтобы проект оказался прибыльным в размене 250000 тыс. руб. Исходя из этих условий и данных финансово-экономической модели, запишем формальные исходные данные для расчета степени риска неэффективности данного ИСП:
– это прибыль в 301184 тыс. руб. Установленное предприятием условие – это то, чтобы проект оказался прибыльным в размене 250000 тыс. руб. Исходя из этих условий и данных финансово-экономической модели, запишем формальные исходные данные для расчета степени риска неэффективности данного ИСП:
 (1)
(1)
Предполагая, что нечеткое число  близко к треугольному виду, запишем для него функцию принадлежности:
близко к треугольному виду, запишем для него функцию принадлежности:
 (2)
(2)
Перейдем к оценке риска инвестиций – Risk (G). На рис. 1-4 изображены функции принадлежности  и критериального значения
и критериального значения  .
.
-
как интервальное значение NPV = [NPVmin, NPVmax];




Рисунок 1 – Оценка риска по интервальному значению NPV
-
как треугольно-симметричное нечеткое число NPV = NPVav
±
D;




Рисунок 2 – Оценка риска по треугольно-симметричному нечеткому числу NPV
-
как треугольное число произвольного вида NPV = (NPVmin, NPVav, NPVmax);




Рисунок 3 – Оценка риска по треугольно-произвольному нечеткому числу NPV
-
как нечеткое число произвольного вида NPV = {NPVa; a® [NPVamin, NPVamax]}, т.е. как набор интервалов по каждому выбранному уровню принадлежности a.



Рисунок 4 – Оценка риска по нечёткому числу общего вида NPV
На рисунках представлено графическое изображение соотношение NPV и критерия эффективности (нечеткого числа, а также величины  ). Зона слева – это область неэффективных инвестиций. Для нашего проекта величина
). Зона слева – это область неэффективных инвестиций. Для нашего проекта величина  расположена таким образом, что
расположена таким образом, что  . Тогда, получим, что
. Тогда, получим, что  ;
;  ;
;  [4].
[4].
По результатам проведённого исследования остановимся на следующих важных моментах. Во-первых, подрядные организации и девелоперы, как правило, склонны сосредотачиваться на обеспечении финансовой жизнеспособности проекта в ходе технико-экономического обоснования. Проект считается экономически целесообразным, если ожидаемый доход соответствует или превышает приемлемый заранее определенный уровень доходности на первоначальные инвестиции организации. Во-вторых, автор обращает внимание на то, что применение той или иной методики расчёта неопределённости ИСП не гарантирует однозначного результата и не избавляет на все 100% от неопределённости. Детальное описание вычисления показателей эффективности ИСП на основе вышеприведённых шести подходов указывает на противоречивый характер как полученных результатов, так и концептуальных основ всего существующего разнообразия методов оценки рисков.
Библиографический список
- Sherif Mohamed, Alison K. McCowan, “Modelling project investment decisions under uncertainty using possibility theory”, International Journal of Project Management, pp. 231-241, 2001.
-
Стадникова Т. А. Нечёткое отображение как инструмент для расчёта ожидаемой эффективности инвестиционного проекта в условиях неопределённости // Журнал научных публикаций аспирантов и докторантов, г. Курск, 2012. – №11. – с 10-14.
-
Harvard Business Review. Управление проектами. “Альпина Бизнес Букс”, — 2009. 189 с.
-
Недосекин А.О. Нечетко-множественный анализ риска фондовых инвестиций // URL: http://sedok.narod.ru/sc_group.html (дата обращения: 06.11.2013).
