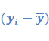В образовании можно и нужно применять интересные статистические методы в преподавании как экономических, так и технических дисциплин. Применение математических методов в информатике позволяет систематизировать информацию, исследовать ее в разных ракурсах, анализировать тенденции развивающиеся во времени в информационных системах.
Примером логического анализа проблемы с помощью математико-статистического метода. является исследование вопросов связанных с информационными технологиями. с применением нормированных разностей и линейного коэффициента корреляции.
Представленные для анализа данные.
Таблица 1:Характеристика компьютерных систем с фирменными брендами.
| бренд- неймфирмы-производителя
(отсортированные по баллам) |
баллы, присвоенныеэкспертами
xj |
время выполнения типовой операции сек.
yi |
| D | 1 | 0,4 |
| Sh | 3 | 0,6 |
| M | 4 | 0,5 |
| S | 4 | 0,8 |
| I | 5 | 0,9 |
| F | 9 | 0,9 |
| J | 10 | 0,8 |
| 36:7=5,1 | 4,9:7=0,7 |
Важно устанавливать степень линейности связей. Для этого существует критерий линейности. Коэффициент линейности должен быть больше 50% или 0,5.
Линейной связи нет(min) ;
Строго линейная связь(max)
Пороговый уровень линейной связи 0,5. Критерий линейной корреляции.
Рисунок 1-Формы линейных связей.
Линейная связь между признаками – это строгая функциональная связь между признаками. Тенденции синхронного прямолинейного возрастания (убывания) или взаимообратный процесс, имеющий линейный характер.[1]
Рассчитаем нормированную разность между признаками ,обозначающие баллы выставленные экспертами.
Матрица нормированных разностей между фирмами по первому исследуемому признаку- баллы экспертов.
Нормированная разность по своей сути относительный показатель координации, покажет отношение разности между координатами двух признаков к среднеквадратическому отклонению таблицы(то есть среднее отклонение исходных элементов таблицы от средней лини направляющей линии или среднего потока).Большее значение нормированной разности означает большую разность между признаками приходящихся на единицу среднеквадратического отклонения таблицы(например баллами и секундами и пр.).
dij=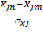
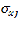-среднеквадратическое отклонение признаков (по столбцам) Xj
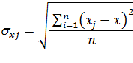
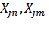абсолютная разность значений пары признаков у единиц совокупности с соответствующими порядковыми расположениями в столбце j.
Нормированная разность по среднеквадратическому отклонению. Нормирование – в долях снимает натуральные единицы измерения и позволяет работать с признаками, измеряемыми разными единицами измерения. [1]
Таблица 2-Нормированные разности между экономическими объектами(показателями)
D |
SH |
M |
S |
I |
F |
J |
|
| D |
- |
0,673 |
1,003 |
1,003 |
1,335 |
2,669 |
3,003 |
| SH |
0,673 |
- |
0,334 |
0,334 |
0,667 |
2,002 |
2,669 |
| M |
1,003 |
0,334 |
- |
0,000 |
0,334 |
1,668 |
2,002 |
| S |
1,003 |
0,334 |
0,000 |
- |
0,334 |
1,668 |
2,002 |
| I |
1,335 |
0,667 |
0,334 |
0,334 |
- |
1,335 |
1,668 |
| F |
2,669 |
2,002 |
1,668 |
1,668 |
1,335 |
- |
0,334 |
| J |
3,003 |
2,669 |
2,002 |
2,002 |
1,668 |
0,334 |
- |
= 5,1
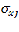= 2,997 баллов
Самая большая поляризация, согласно нормированных разностей (3,003)между фирмами J и D.
Интерференция(совпадение признаков) между элементами S и M.
С помощью нормированных разностей можно определить евклидовы расстояния, на значении которых основан кластерный анализ.
Теперь можно установить линейную тенденцию в корреляции между двумя признаками xi и yi рассчитав линейный коэффициент парной корреляции.
Этот коэффициент основан на нормированных отклонениях.
dx=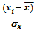
; dy=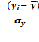
Среднее произведение нормированных отклонений пары признаков =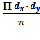
есть линейный коэффициент корреляции.[1,2]
r =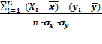 
Для подсчета линейного коэффициента корреляции образуем вспомогательную таблицу.
Таблица 3-Расчетая таблица по признакам x и y .
 |
 |
 |
 |
×
|
|
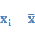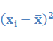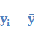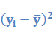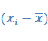
| D | 4,1 | 16,81 | 0,3 | 0,09 | 1,23 |
| Sh | 2,1 | 5,76 | 0,1 | 0,01 | 0,21 |
| M | 1,1 | 1,21 | 0,2 | 0,04 | 0,22 |
| S | 1,1 | 1,21 | 0,1 | 0,01 | 0,11 |
| I | 0,1 | 0,01 | 0,2 | 0,04 | 0,02 |
| F | 3,9 | 15,21 | 0,2 | 0,04 | 0,78 |
| J | 4,9 | 24,01 | 0,1 | 0,01 | 0,49 |
| S | 17,3 | 64,22 | 1,2 | 0,24 | 3,06 |
= 
=
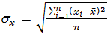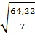3,03
=
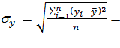
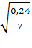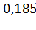
r =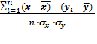 
= 
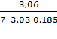=3,06/3,92= 0,78
Линейная зависимость сильная. Наблюдается тенденция увеличения значений, как показателя 1,так и показателя 2.Если один упорядоченный ряд ,а второй ряд увеличивается по неравномерной прогрессии, то есть элементы не только увеличиваются но и уменьшаются, линейный коэффициент будет меньше, в зависимости от количества элементов, не подходящих под линию соответствующей упорядоченности.[1,2]
Представленный пример имеет малую градацию признаков, но в информационных технологиях мы имеем дело с огромными массивами информации равные сотням, а то и тысячи позиций. Математические и статистические методы помогут вывести четкое числовое значение зависимостей соответствующих признаков, подтвердят или опровергнут выдвигаемые гипотезы, укажут на прямую и обратную связь основных показателей.
В образовании симбиоз математики и информатики поможет научить логически мыслить, овладеть богатым опытом применения математических и статистических методов в массивах информации, информативно насытиться новыми знаниями.
Данные методы помогут в маркетинговых исследованиях самого различного характера.
Конечно, ставя перед собой экономические задачи, основной целью использования коэффициентов будет исследование тренда экономического явления.
Библиографический список
- Статистический словарь; М:,Энциклопедия,2010
- Статистические методы в экономике. Краткий справочник для специалистов; М:,Энциклопедия,2007