Производственная функция является математическим , а иногда и графический способ измерения эффективности производства, она рассматривает отношения между двумя или более факторами. Производственная функция применяется для анализа влияния различных факторов на объем прибыли в определенный момент времени, а также для прогнозирования соотношений объема факторов и объемов выпуска в различные моменты времени.

Функциональная форма Кобба-Дугласа производства широко используется в экономике. Она был предложена Кнутом Виксель (1851 – 1926), и проверена на статистических данных Чарльзом Коббом и Полом Дугласом в 1928 году. В 1928 году Чарльз Кобб и Пол Дуглас опубликовали исследование, в котором они смоделировали рост американской экономика в период 1899 г. – 1922 г. Они брали два фактора, которые по их мнению влияли на общий объем производства. В то время как многие другие факторы влияли на экономические показатели, но их модель оказалась удивительно точной. Функция, которую они использовали для моделирования производства, была вида:

P – общий объем производства (денежная стоимость всех товаров, произведенных в течение года)

L – рабочая сила (общее количество рабочих за год)

K – входной капитал (денежная стоимость всех машин, оборудования и зданий)

А – число масштаба

α и β являются выходной эластичностью труда и капитала, соответственно.

Постановка задачи

Имеются статистические данные с 1998 – 2015 гг. о реальной выручке, капитале и численности рабочих в компании ПАО «Газпром». Наша цель построить производственную функцию по этим данным.

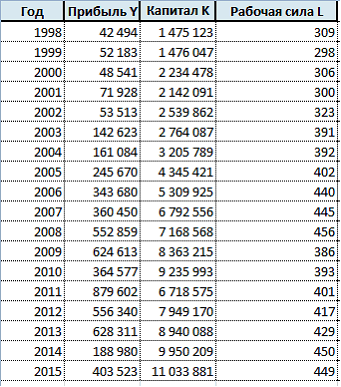
Введем исходные статистические данные в таблицу MO Excel.

Наша задача состоит в построении ПФ Кобба-Дугласа  , где  , следовательно, необходимо найти параметры . Будем использовать метод наименьших квадратов. Тогда задача будем выглядеть следующим образом:

.

При ограничениях:

,.

Где  - отклонение расчетного значения от фактического ( ).

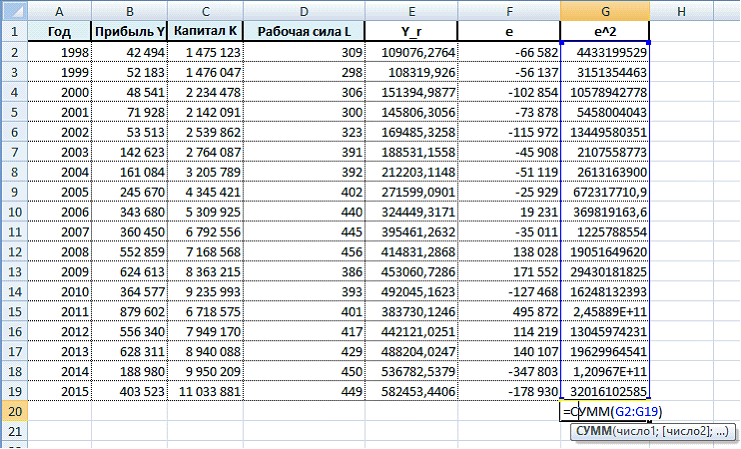
Получили следующую задачу оптимизации :

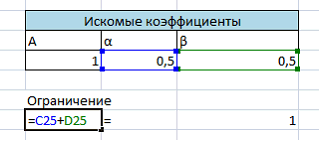
Используя надстройку «Поиск решения» Excel решим следующую задачу оптимизации для нахождения параметров целевой функции:

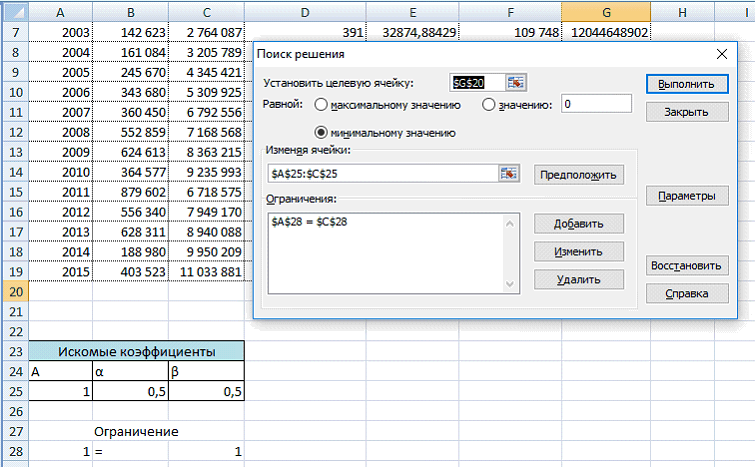
Были получены следующие результаты:

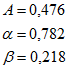
Следовательно, производственная функция Кобба-Дугласа выглядит следующим образом:

и это означает, что доля труда в совокупном продукте составляет 78,1%, а доля капитала — 21,8%.

Для того, чтобы показать, что при различных сочетаний факторов производства , объем выпуска может оставаться одним и тем же, построим изокванты соответствующие выпуску C. Уравнение изокванты будет имеет вид:

.

Построим изокванты , соответствующие выпуску 300 000 ,320 000, 360 000, 400 000 млн. рублей соответственно.

Т.е., если Y1=300 000. Тогда . Найдем K, как функцию от L. Функция будет иметь вид:

Вычислим их и построим график:

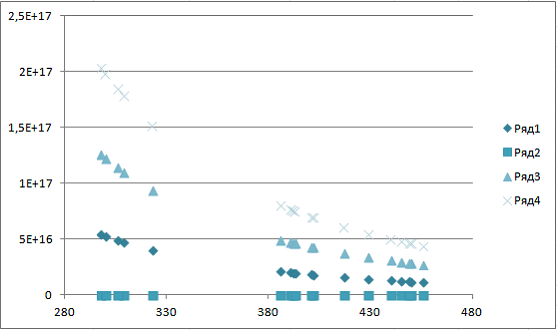
Из графика мы видем, что изокванты не пересекаются и каждая следующая изокванта, проходит дальше от начала координат.

Для производственной функции Кобба-Дугласа покажем, что эластичность выпуска по капиталу равна показателю степени при капитале.

Т.е. получили, что эластичность выпуска по капиталу равна 0,782, что равно показателю степени при капитале.

Вывод: Построена ПФ Кобба-Дугласа по статистическим данным, используя метод наименьших квадратов. Функция Кобба-Дугласа имеет вид: . Построены изокванты для ПФ Кобба-Дугласа. Для ПФ Кобба-Дугласа показано, что эластичность выпуска по капиталу равна показателю стпени при капитале.

1. Электронный ресурс. URL http://www.gazprom.ru/
2. Галиаскарова Г.Р.  Практикум по математической экономике . Учебное пособие . Уфа: РИЦ БашГУ , 2011.-88c.

Все статьи автора «Алексеева Кристина Владимировна»