Практическая деятельность современного человека в той или иной степени неразрывно связана с финансовыми вычислениями, основные методы которых позволяет изучить финансовая математика.
Финансовая математика – это необходимые расчёты инвестиционных и торговых операций во времени с учётом инфляции; юридических и фактических условий выполнения договоров и курса валют, а также расчёты об их доходности, выстроенных в систему. Данная система исследует результаты и параметры финансовых и коммерческих операций, акцентируя внимание на обыкновения, сложившиеся в мире бизнеса.
Можно придти к промежуточному выводу, что финансовая математика занимает одно из основных мест в банковской сфере, так как смысловые единицы определения финансовой математики («коммерческие операции», «инфляция», «курс валют» и т.д.) являются взаимозаимствованными .
Рассмотрим применение финансовой математики в отечественной банковской сфере, а главным термином, через использование которого и будет строиться вся дальнейшая работа, будет «процент».
С 1998 года российские кредитные организации и банки применяют точный процент с базой в 365 или 366 дней. В Российской банковской системе чаще всего первый и последний день месяца принимают за один день. В связи с тем, что процент начисляется автоматически, сразу после открытия банковского отделения. Отсюда и вытекает, то, что сдача депозита рассчитанного на один месяц происходит на 31 –ый день со дня денежного вложения. Это не является особенностью отечественной банковской системы, это всемирная практика. Если взята ссуда на период с 13 июля по 19 сентября, то число дней ссуды вычисляется так: в июле – 18 дней (31 -13 =18) + в августе – 31 день + в сентябре – 19 дней. Всего 68 дней. Если взята 29 января 2012 г. ссуда на один месяц, то отдавать ее придется на 31-й день, то есть 1 марта.
Пример сферы применения точных простых процентов: При краткосрочных операциях используется так называемая промежуточная процентная ставка, под которой понимается годовая процентная ставка, приведенная к сроку вложения денежных средств. Математически промежуточная процентная ставка равна доле годовой процентной ставки. Формула наращения простых процентов с использованием промежуточной процентной ставки имеет следующий вид:
FV = PV (1 + f • r),
или
FV = PV (1 + t • r / Т),
где f=t/T;
t — срок вложения денежных средств (при этом день вложения и день изъятия денежных средств принимаются за один день); Т — расчетное количество дней в году.
При долгосрочных операциях начисление простых процентов рассчитывается по формуле:
FV = PV (1 + r • n),
где n — срок вложения денежных средств (в годах).
Целесообразной сферой использования сложных процентов выступают длительные операции – временными рамками, превосходящими 12 месяцев, в том числе подразумевающее внутригодовое начисление процентов.
Благодаря возможности получения подобных данных происходит составление отчётной документации всего мирового финансового рынка. Это делает востребованными специалистов по финансовой математике в целом и узко специализирующихся на вычислениях точных простых процентов с точным числом дней.
Происхождение сложного процента и срочного вклада:
1) Сложный процент восстанавливает справедливость, он уравнивает ” так называемого ленивого” и “активного” клиентов. Переоформление вклада ничего не приносит банкиру, кроме дополнительных рисков, поэтому он сам должен начислять сложный процент.
2) Во избежание процедуры изъятия и повторного вклада обе стороны
кредитной или депозитной сделки заранее договариваются об использовании сложных процентов и срочных вкладов в совокупности. В стабильных экономических условиях при многолетнем сроке кредита применение сложного процента является неписаным стандартом. Но год – это большой срок. Поэтому многие российские и иностранные банки
кредитных договорах используют следующие формулировки:
• “Ежеквартально сумма вклада увеличивается на … процентов” или
• “Проценты по вкладу капитализируются каждые три месяца” или
• “Сумма процентов по вкладу прибавляется к основному вкладу раз в три
месяца”.
Рациональный подход к применению научных знаний заставляет учёных самых различных дисциплин брать на вооружение достижения других, даже даже несмежных с ними наук. И если первоначально финансовая математика находила применение только в рамках экономики, то во второй половине 20 века расчёты процентной прибыли и прироста капитала начали применяться сначала в статистике, а затем и в гуманитарных науках.
Благодаря возможности обращаться разного рода цифровым данным и расчётам на базе формул финансовой математики была сформулирована статистическая основа для составления баз данных и прогнозирования финансовых кризисов на всех видах современных рынков. Своевременность и достоверность выполняемых вычислений сводят к минимуму человеческий фактор в составлении прогнозов на финансовый год для практически любых компаний и предприятий.
Значительный интерес вызывает тот факт, что некоторые учёные гуманитарного направления взяли на вооружение в своих работах элементы финансовой математики. К примеру, латвийский ученый Альвидас Фландрис при составлении монографии советского периода по экономике Латвии проводил расчёты прибыли и доходности на основе методов финансовой математики
Применение в финансово-математических исследованиях информационных технологий в нынешних условиях просто необходимы. Мультимедиа и достижения it-сферы значительно облегчают математикам работу с источниками и отчётным материалом, позволяют вести научные диспуты и конференции дистанционно. Визуальное оформление получаемое при использовании информационных технологий повышают репрезентативность всех современных и финансово-математических исследований.
И в заключении рассмотрим несколько задач, иллюстрирующих практическую значимость финансово-математических расчетов.
В кредитном договоре на сумму 3500000 руб. и сроком на 5 лет зафиксирована ставка сложных процентов, равная 40% годовых. Определите общую сумму выплат за весь период кредитования.
Воспользуемся формулой наращения для сложных процентов:
![]()
Через 5 лет предприятию будет выплачена сумма 3500000 руб. Определить первоначальную величину взноса при условии, сто применяется сложная процентная ставка 40% годовых.
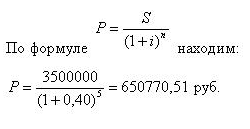
Библиографический список
- Криничанский К.В. Математика финансового менеджмента – М: Дело и сервис, 2001.
- Ковалев В. В., Уланов В.А. Курс финансовых вычислений и практик – М: Журнал «Финансы и Статистика», 2001.
- Кочович Е. Финансовая математика с задачами и решениями. – М: Журнал «Финансы и статистика», 2004.
- Сухих Е.С., Зеленина Л.И. Эконометрическое моделирование как эффективный метод анализа в научных исследованиях студентов // Современная педагогика. 2014. № 12, С. 75-79.
- Федькушова С.И., Зеленина Л.И. Математические методы обработки данных в научно-исследовательских работах студентов // Современная педагогика. 2015. № 1 (26) с.39-44 [Электронный ресурс]. URL: http://pedagogika.snauka.ru/2015/01/2894 (дата обращения: 07.01.2015).
