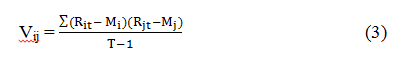Особое значение для предприятий в современных условиях приобретают операции с ценными бумагами. Хозяйствующим субъектам предоставлено право свободно продавать и покупать свои и приобретенные ценные бумаги. В ходе аудиторской проверки аудитор должен проверить не только операции по эмиссии ценных бумаг организации, но и финансовые вложения в виде инвестиций в финансовые инструменты.
При проверке операций с ценными бумагами, представляющими финансовые вложения, аудитору необходимо убедиться в наличии правильно оформленных документов, подтверждающих право на обладание приобретенными ценными бумагами, и оценить их способность приносить предприятию экономические выгоды в виде процентов, дивидендов либо прироста стоимости.
Однако, есть риск получить убыток по операциям с финансовыми вложениями, который может привести организацию к банкротству. В этой связи при проверке операций с ценными бумагами аудитору следует изучить доходность и уровень риска получения дохода. При этом следует иметь ввиду, что чем выше степень доходности актива, тем выше степень риска.
При аудите финансовых вложений в ценные бумаги аудитору необходимо проверить доходность, риск, правильность вложений в те или иные инструменты и предложить повысить эффективность вложений (если требуется) либо избавиться от неэффективных вложений.
Среди классических моделей оценки риска финансовых вложений мы предлагаем выделить методику определения риска при помощи модели Марковица. Основы теоретического подхода к анализу и формированию инвестиционного портфеля из рисковых активов, базирующегося на идее диверсификации, были разработаны американским ученным Г. Марковицем. Он разработал математическую модель, демонстрирующую, как инвесторы могут снизить риск при заданной ставке доходности.
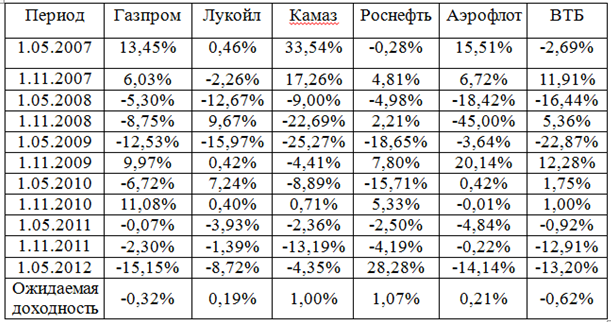
Рассмотрим задачу минимизации риска портфеля при заданном уровне его доходности, то есть оптимизации портфеля ценных бумаг. Предположим, что инвестор располагает информацией за шесть лет (с 1.05.2007 по 1.05.2012) с периодичностью в месяц, отражающей динамику курсов следующих эмитентов: ОАО «Газпром», ОАО «Лукойл», ОАО «Камаз», ОАО «Роснефть», ОАО «Аэрофлот», ОАО «ВТБ».
Таблица 1. Динамика курсов акций эмитентов
Первым шагом по оценке риска портфеля акций будет проведение экономико-статистического анализа динамики курсов акций эмитентов. Рассчитаем величину доходности акций. Для этого используем формулу:
где Сjt+1 – усредненная цена j-ой бумаги в месяце t+1;
Сjt – усредненная цена j-ой бумаги в месяце t.
Рассчитаем ожидаемую доходность по формуле:
В итоге получаем следующие результаты, представленные в таблице 2
Таблица 2. Ожидаемая доходность ценных бумаг
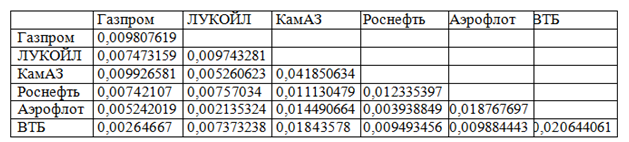
Расчет оценки ковариаций между ценными бумагами данных эмитентов по следующей формуле, результаты приведены в таблице 3:
Таблица 3
Результат расчета ковариации между акциями, входящими в портфель
Из нашего набора ценных бумаг можно сформировать бесконечное число портфелей с разными пропорциями вложений в каждую акцию. Инвестор может купить акции только одного эмитента, или же, например, 40% акций ОАО «Газпром», 35% ОАО «Роснефть» и 25% ОАО «ВТБ». Весь набор портфелей разных пропорций называется эффективным множеством.
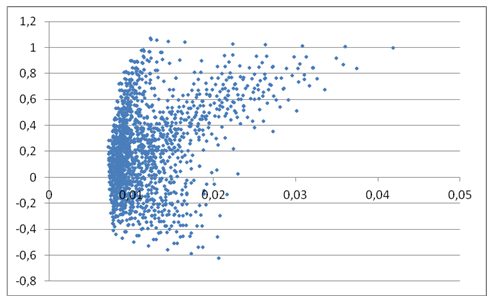
Рассчитав доходности каждого портфеля и стандартное отклонение достижимого множества портфелей (расчет произведен для структуры портфеля с интервалом 10%), мы смогли построить точечную диаграмму, представленную на рисунке 1.
Рассматривая точечную диаграмму, можно сделать вывод, что точка, находящаяся с левого края (имеющая минимальное стандартное отклонение), представляет собой минимально рисковый портфель. Для нашего портфеля наименьшее значение равно 0,0072%, доходность 0,23%, он предполагает вложения: 10% в акции Газпром, 50% Лукойл, 10% Роснефть и 30% Аэрофлот. Если же рассматривать портфель с наибольшей доходностью, то это будет портфель, состоящий из 70% акций Газпрома, 20% акций ЛУКОЙЛа и 10% акций КамАЗа. Этот портфель имеет доходность 1,07% и риск 0,013%.
Рис. 1. Достижимое множество для выбранного портфеля
Используя коэффициент Шарпа, мы определили отношение доходности каждого портфеля эффективного множества и соответствующего ему стандартного отклонения. Получив максимальное значение (90,654) мы можем утверждать, что самый оптимальный портфель на нашей точечной диаграмме имеет портфель, у которого вложения соответствуют: 80% акций Роснефти, а 20% акций Аэрофлота.
После проведения всех расчетов мы можем сделать вывод, что модель Марковица может применяться только на первоначальном этапе формирования портфеля. С ее помощью мы можем провести анализ основных характеристик: математического ожидания, дисперсии и ковариации доходности акций различных эмитентов. Но самым главным в концепции Марковица является диверсификация. Диверсификация портфеля предполагает включение в состав портфеля различных финансовых инструментов таким образом, чтобы снизить корреляцию их доходности. Но, на практике Российского рынка мы можем увидеть, что активов с малой и отрицательной корреляцией существует совсем немного. Все из-за того, что рынок двигается, в целом, в одном направлении. Для того чтобы найти действительно рассогласованные типы активов, нужно искать в разных классах: акциях, облигациях, недвижимости, валютах и т.д.