Научный руководитель: Бакуменко Людмила Петровна, профессор, доктор экономических наук
Здоровье населения является показателем внешнего и внутреннего социального благополучия, а также косвенным показателем национальной безопасности. Для создания здорового общества, прежде всего, необходимо особое внимание уделять детскому населению – важнейшему резерву производительных сил [5].
В последние годы в России отмечены неблагоприятные тенденции в состоянии здоровья новорожденных, физическом развитии и репродуктивном здоровье детей, регистрируется рост заболеваемости и инвалидности детей.
Проведем многомерный статистический анализ, применяемый для изучения взаимосвязей между значениями количественных переменных, так называемый метод главных компонент.
Метод главных компонент (англ. principal component analysis, PCA) – один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации.
Сформируем главные компоненты путем выделения наиболее значимых факторов, построим уравнения регрессии на главных компонентах.
Рассмотрим следующие показатели:
y – заболеваемость детей первого года жизни;
паразитарные болезни;
– новообразования;
отдельные нарушения, вовлекающие иммунный механизм;
поражение головного мозга;
болезни крови;
поражение легких;
поражение кишечника;
болезни мышц;
нарушения мочеиспускания;
отдельные состояния, возникающие в перинатальном периоде;
пороки развития;
симптомы, признаки и половые отклонения от нормы, выявленные при клинических и лабораторных исследованиях, не классифицированные в других рубриках;
другие последствия внешних причин.
Применим метод главных компонент к исходным данным, реализуем в прикладной программе STATISTICA с помощью пакета «Факторный анализ» (Многомерный разведочный анализ).
Для анализа выберем только факторные признаки (без результативного), именно их будем объединять в факторы. Максимальным числом факторов назначим 5, а мин. собственным значением 1. Отобразим полученные результаты в таблице собственных значений (табл. 1).
Таблица 1 – Собственные значения
|
Собственные значения (Заболевания) Выделение: Главные компоненты |
||||
|
Соб. зн. |
% общей дисп. |
Кумулятивн. % |
Кумулятивн. % |
|
|
1 |
6,430284 |
49,46372 |
6,43028 |
49,46372 |
|
2 |
1,450486 |
11,15759 |
7,88077 |
60,62131 |
|
3 |
1,286332 |
9,89486 |
9,16710 |
70,51617 |
|
4 |
1,027715 |
7,90550 |
10,19482 |
78,42167 |
С помощью МГК было выделено всего 4 фактора. В данном случае 49,4% общей дисперсии объясняется первым фактором, 11,1% – вторым фактором, 9,8% – третьим фактором, а 7,9 – четвертым. Вместе все факторы объясняют 78,2% дисперсии.
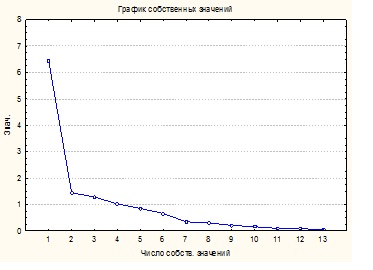
Для более наглядного представления собственных значений можно применить график каменистой осыпи (рис. 1).
Рисунок 1 – График каменистой осыпи
Оценим значения факторных нагрузок и вычислим коэффициенты информативности для случая с 4 факторами. Применяем метод без вращения (табл. 2).
Таблица 2 – Факторные нагрузки без вращения
|
Фактор.нагрузки (без вращ.) (Заболевания) Выделение: Главные компоненты (Отмечены нагрузки >,700000) |
||||
|
Фактор 1 |
Фактор 2 |
Фактор 3 |
Фактор 4 |
|
|
x1 |
-0,906171 |
0,168169 |
-0,069067 |
0,103201 |
|
x2 |
-0,064039 |
0,177556 |
-0,624607 |
0,352374 |
|
x3 |
-0,715111 |
0,454131 |
-0,260315 |
-0,200431 |
|
x4 |
-0,796530 |
0,058636 |
0,223904 |
0,322326 |
|
x5 |
-0,131180 |
0,149089 |
0,719122 |
-0,248879 |
|
x6 |
-0,935172 |
-0,165231 |
-0,078377 |
-0,161054 |
|
x7 |
-0,882400 |
-0,106081 |
0,140442 |
0,089172 |
|
x8 |
-0,751265 |
-0,130523 |
0,288880 |
0,425364 |
|
x9 |
-0,385673 |
-0,631885 |
-0,249897 |
-0,565416 |
|
x10 |
-0,696263 |
0,459002 |
-0,223151 |
-0,221674 |
|
x11 |
-0,844809 |
-0,190434 |
-0,083617 |
0,049296 |
|
x12 |
-0,330929 |
0,573588 |
0,165863 |
-0,317335 |
|
x13 |
-0,876165 |
-0,357713 |
0,018153 |
-0,009931 |
|
Общ.дис. |
6,430284 |
1,450486 |
1,286332 |
1,027715 |
|
Доля общ |
0,494637 |
0,111576 |
0,098949 |
0,079055 |
Главная компонента считается информативной, если коэффициент достаточно высокий Ки ≥ 0,5 ÷ 0,95. Необходимо использовать вращения для факторных нагрузок, применяя вращение «варимакс исходных». Получаем более высокие коэффициенты информативности (табл. 3).
Таблица 3 – Факторные нагрузки при «варимакс исходных»
|
Фактор 1 |
Фактор 2 |
Фактор 3 |
Фактор 4 |
|
|
x1 |
0,745065 |
0,542644 |
0,080362 |
0,093835 |
|
x2 |
0,031837 |
0,186466 |
0,701589 |
-0,148044 |
|
x3 |
0,340174 |
0,830188 |
0,097464 |
0,105476 |
|
x4 |
0,848451 |
0,242404 |
-0,071859 |
-0,090182 |
|
x5 |
0,130303 |
0,078797 |
0,764445 |
-0,104636 |
|
x6 |
0,715123 |
0,424038 |
-0,008777 |
0,592588 |
|
x7 |
0,826600 |
0,281388 |
-0,093396 |
0,215385 |
|
x8 |
0,914460 |
0,024115 |
-0,069532 |
-0,064570 |
|
x9 |
0,132033 |
0,025694 |
0,002485 |
0,955022 |
|
x10 |
0,322431 |
0,823033 |
0,054825 |
0,100251 |
|
x11 |
0,742248 |
0,278242 |
0,094237 |
0,349511 |
|
x12 |
0,043073 |
0,660955 |
-0,335518 |
0,624259 |
|
x13 |
0,800236 |
0,168751 |
-0,012321 |
0,476495 |
|
Общ.дис. |
4,754165 |
2,563782 |
1,235976 |
1,640894 |
|
Доля общ |
0,365705 |
0,197214 |
0,095075 |
0,126223 |
Нормализованные коэффициенты информативности получаются достаточно хорошими для всех четырех факторов (табл. 4) [5]. Поэтому можно считать, что все факторы оказались информативными.
Таблица 4 – Коэффициенты информативности
|
Ки1 |
Ки2 |
Ки3 |
Ки4 |
|
0,94595 |
0,533039 |
0,871055 |
0,555835 |
Теперь рассмотрим переменные, которые вошли в каждую главную компоненту.
В первую главную компоненту вошли:
паразитарные болезни;
поражение головного мозга;
поражение легких;
поражение кишечника;
болезни мышц;
пороки развития;
отравления.
Название фактора – инфекционные заболевания органов.
Во вторую главную компоненту вошли:
отдельные нарушения, вовлекающие иммунный механизм;
отдельные состояния, возникающие в перинатальном периоде.
Название фактора – отдельные нарушения состояния здоровья.
В третью главную компоненту вошли:
– новообразования;
болезни крови;
Название фактора – болезни кровяной системы.
В четвертую главную компоненту вошли:
нарушения мочеиспускания;
симптомы, признаки и половые отклонения от нормы, выявленные при клинических и лабораторных исследованиях.
Название фактора – заболевания мочеполовой системы.
Теперь для этих факторов получаем значения факторов и для них проводим регрессионный анализ для определения степени влияния каждого фактора на результативный признак – заболеваемость детей первого года жизни. Выполним пошаговую регрессию с исключением и выводим результаты (табл. 5).
Таблица 5 – Итоги множественной регрессии
|
Итоги регрессии для зависимой переменной: y (Заболевания) R= ,98766442 R2= ,97548100 Скорректир. R2= ,97489722 F(2,84)=171,0 p |
||||||
|
БЕТА |
Стд.Ош. |
B |
Стд.Ош. |
t(84) |
p-уров. |
|
|
Св.член |
52786,9 |
794,6964 |
66,4240 |
0,000000 |
||
|
ФАКТОР1 |
-0,983999 |
0,017085 |
-46035,7 |
799,3034 |
-57,5947 |
0,000000 |
|
ФАКТОР4 |
-0,085016 |
0,017085 |
-3977,4 |
799,3034 |
-4,9761 |
0,000003 |
В результате вычислений получили, что значимыми являются только 2 фактора из 4-ех: фактор 1 – инфекционные заболевания органов и фактор 4 – заболевания мочеполовой системы.
В итоге получаем уравнение:
y = 52786,9 – 46035,7f1 – 3977,4f4
R2 = 0,97
Коэффициент детерминации (R2) показывает, что 97% вариации результативного признака объясняется включенными в модель переменными (факторами 1, 4), остальные же 3% вариации объясняется неучтёнными в модели факторами [2].
Модель можно считать значимой, так как фактическое значение F-критерия Фишера превышает критическое при заданных степенях свободы и уровне значимости 95%.
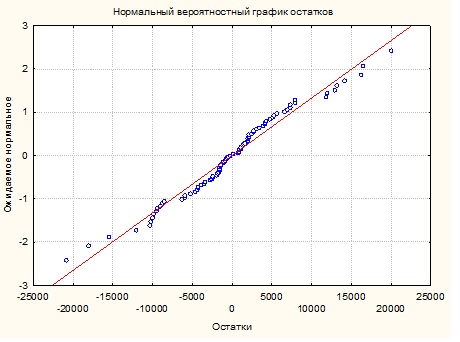
Рассмотрим вероятностный график остатков для произведенных расчетов множественной регрессии (рис. 2).
Рисунок 2 – Нормальный вероятностный график
По графику остатков можно увидеть, что значения остатков распределены равномерно и достаточно хорошо ложатся на график нормальных остатков.
Коэффициенты уравнения показывают, насколько изменится значение результативного признака при изменении величины факторного на 1 единицу. С уменьшением инфекционных заболеваний органов (f1) на 1 единицу значение результативного признака уменьшится на 46035,7 ед. С уменьшением числа заболеваний мочеполовой системы на 1 единицу заболеваемость детей первого года жизни сократится на 3977,4 ед.
Библиографический список
- Безруких М.М., Сонькин В.Д., Фарбер Д.А. Возрастная физиология (физиология развития ребенка): учебное пособие. – М.: Академия, 2012. – 416 с.
- Гавриленко О. Л., Попова А.Ю., Черныш Е.В. Состояние здоровья детского населения Московской области и комплекс мероприятий, направленных на его улучшение // Здравоохранение РФ. – 2013. – № 1. – С. 34-35.
- Баранов А.А., Альбицкий В.Ю. Основные тенденции здоровья детского населения России. – М.: Союз педиатров России, 2012. – 116 с.
- Бабешко Л.О. Основы эконометрического моделирования : учеб. пособие / Л. О. Бабешко. – Изд. 4-е. – М.: КомКнига, 2012. – 428 с.
- Алексеев А.Р. Экономическая статистика: учебник для вузов / [Алексеев А.Р., Воробьев А.Н., Громыко Г.Л., и др.]; под ред. Ю.Н. Иванова. – М.: ИНФРА-М, 2014. – 734 с.