Объектом исследования в данной работе является производственные показатели строительных компаний России [4].

В зависимости от конкретных задач, решаемых в экономике, или в другой сфере, используется один из методов факторного анализа.

Главными целями факторного анализа являются: сокращение числа переменных (редукция данных) и определение структуры взаимосвязей между переменными, т.е. классификация переменных. Поэтому факторный анализ используется или как метод сокращения данных, или как метод классификации.

В данной работе рассматривается трудоемкость единицы продукции и 13 производственных показателей по 53 предприятиям. А именно, х1 -удельный вес рабочих в составе ППП; х2 -  удельный вес покупных изделий; х3 – коэффициент сменности оборудования; х4 – премии и вознаграждения на одного ребенка; х5 – удельный вес потерь от брака; х6 – фондоотдача; х7 – среднегодовая численность ППП; х8 – среднегодовая стоимость ОПФ; х9 – среднегодовой фонд заработной платы ППП; х10 – фондовооруженность труда; х11 – оборачиваемость нормируемых оборотных средств; х12 – оборачиваемость ненормируемых оборотных средств; х13 – непроизводственные расходы.

Для установления связи между трудоемкостью единицы продукции и производственными показателями предлагается использовать модели, построенные на основе главных компонент. Для реализации поставленной задачи был  выбран метод главных компонент.

Метод главных компонент (разложение Карунена-Лоева, principal component analysis, PCA) является простейшим методом уменьшения размерности в данных. Идея метода заключается в поиске в исходном пространстве гиперплоскости заданной размерности с последующим проектированием выборки на данную гиперплоскость. При этом выбирается та гиперплоскость, ошибка проектирования данных на которую является минимальной в смысле суммы квадратов отклонений  [1].

В качестве математического инструментария использован пакет Statistica.  Statistica — это инструмент разработки пользовательских приложений в бизнесе, экономике, финансах, промышленности, медицине, страховании и других областях [2].

Сначала рассмотрим собственные значения исходных данных, которые представлены в таблице 1.

Таблица 1 – Собственные значения

Дисперсии, выделяемые факторами, названы собственными значениями. В третьей колонке для каждого фактора приводится процент от общей дисперсии.  В соответствии с критерием Кайзера (Kaiser, 1960), необходимо оставить факторы с собственными значениями больше 1 [2]. Из таблицы 1 видно, что все значения больше единицы. Отсюда следует,  что можно выделить четыре основных фактора.

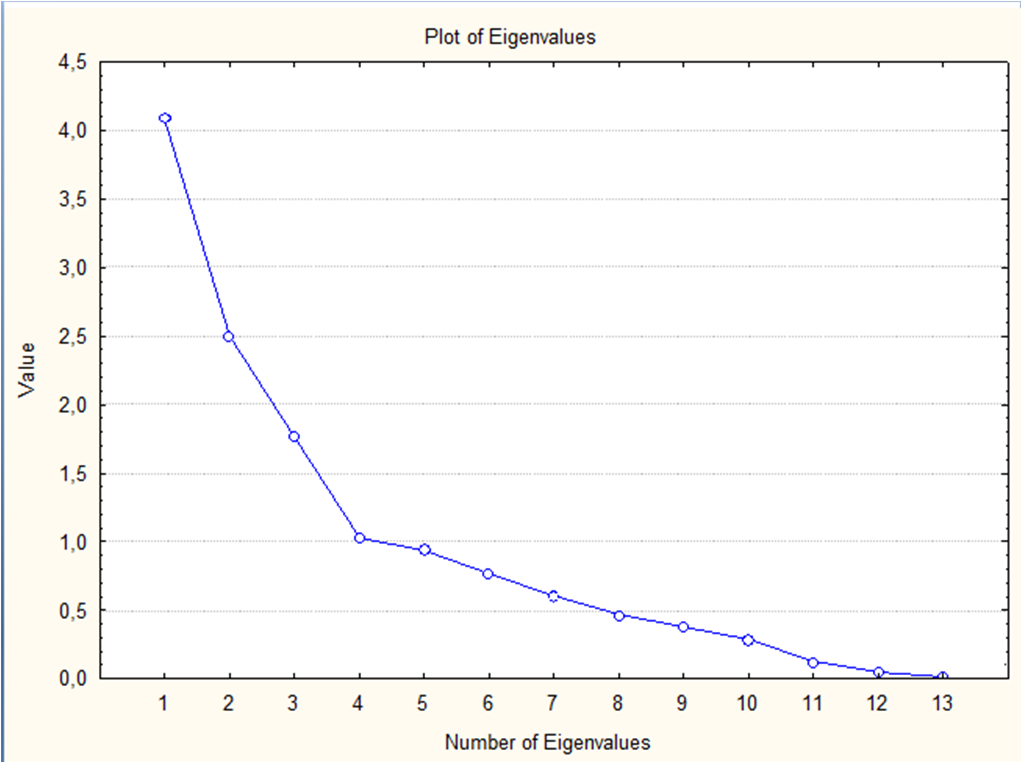
Построим график каменистой осыпи, или собственных значений (рис. 1). Критерий каменистой осыпи является графическим методом, впервые предложенным Кэттелем (Cattell, 1966). [3] По графику можно выделить четыре основных фактора. Осыпание наиболее существенно замедляется на 4 точке, следовательно, можно ограничиться 4 факторами.

Рисунок 1 – График каменистой осыпи

Определим факторные нагрузки, выделим переменные, которые коррелируют с главной компонентой от 0,7.

Таблица 2 – Факторные нагрузки (без вращения оси)

Из таблицы 2 видно, что второй и четвертый фактор оказались не загруженными, следовательно, необходимо произвести вращение факторов (табл. 3).

Таблица 3 – Факторные нагрузки (после вращения)

Цель вращения – получение простой структуры, при которой большинство наблюдений находится вблизи осей координат. При случайной конфигурации наблюдений невозможно получить простую структуру. Возможен выбор различный поворот оси. Выберем вращение квартимах исходный, то есть вращаемые нагрузки не нормализированы.

По-видимому, первый фактор более коррелирует с переменными, чем второй, третий и четвертый. Это следовало ожидать, потому что факторы выделяются последовательно и содержат все меньше и меньше общей дисперсии.

Факторы можно представить в виде трех ортогональных координатных осей. Если на этих осях отметить значения факторных нагрузок, соответствующих каждому из 13 нормированных показателей, то получим 13 точек, каждая из которых характеризует одну из строк матрицы . В результате имеем следующий график на  рисунке 2.

Рисунок 2– Факторные нагрузки

В итоге получаем четыре главных компоненты. Первая главная компонента коррелирует со следующими показателями: Х7 – среднегодовая численность ППП, Х8 – среднегодовая стоимость ОПФ,  Х9 – среднегодовой фонд заработной платы ППП. Поэтому данную компоненту назовем показатели ресурсов предприятия.

Вторая главная компонента коррелирует со следующими показателями: Х1 – удельный вес рабочих в составе ППП, Х11 – оборачиваемость нормируемых оборотных средств, Х13 – непроизводственные расходы. Поэтому данную компоненту назовем показатели трудовых затрат.

Третья главная компонента коррелирует со следующими показателями: Х2 – удельный вес покупных изделий. Поэтому данную компоненту назовем удельный вес покупных изделий.

Четвертая главная компонента коррелирует со следующими показателями: Х10 – фондовооруженность труда. Поэтому данную компоненту назовем фондовооруженность труда.

Рассчитаем коэффициент информативности главных компонент. Затем получаем таблицу 4 с факторными нагрузками.

Таблица 4 – Факторные нагрузки

Как видно из таблицы 4, фактор 1 (показатели ресурсов предприятия) имеет наибольшую информативность, а значит, он оказывает наибольшее влияние на трудоемкость единицы продукции. Наименьшую информативность имеет составляющая  фондовооруженность труда.

Таким образом, после сокращения размерности 13 переменных, характеризующих трудоемкость единицы продукции, наиболее значимыми факторами оказались: составляющая показатели ресурсов предприятия, составляющая показатели трудовых затрат, составляющая удельный вес покупных изделий и составляющая фондовооруженность труда.

Построим регрессию, где зависимыми переменными станут значения факторов. В качестве зависимой переменной укажем «Трудоемкость единицы продукции» (У), в качестве независимых – все остальные. Были получены результаты в виде «Итоговой таблицы регрессии» (Табл. 5). Все переменные в регрессионной модели значимы (p-уровень < 0.05 – подсвечены красным цветом).

Таблица 5 – Итоги регрессии факторного анализа

Коэффициент детерминации показывает, какая доля дисперсии отклика объясняется влиянием предикторов в построенной модели. Чем ближе R2 к 1, тем лучше модель.

Гипотеза об отсутствии линейной связи отклоняется, т.к. в данном случае значение F-статистики = 20, 992 при уровне значимости p < 0,00000.

Итак, для данной модели в результате проведения множественной регрессии, зависимая переменная  «Трудоемкость единицы продукции» представима как:

Итак, как видно из уравнения, такие факторы, как f3 и f4 оказывают отрицательное влияние на трудоемкость единицы продукции. Так при увеличении факторов f1 и f2 трудоемкость единицы продукции будет возрастет.

Выполним построение «Гистограммы остатков», которая представлена на рисунке 3.

Рисунок  3 – Гистограмма остатков

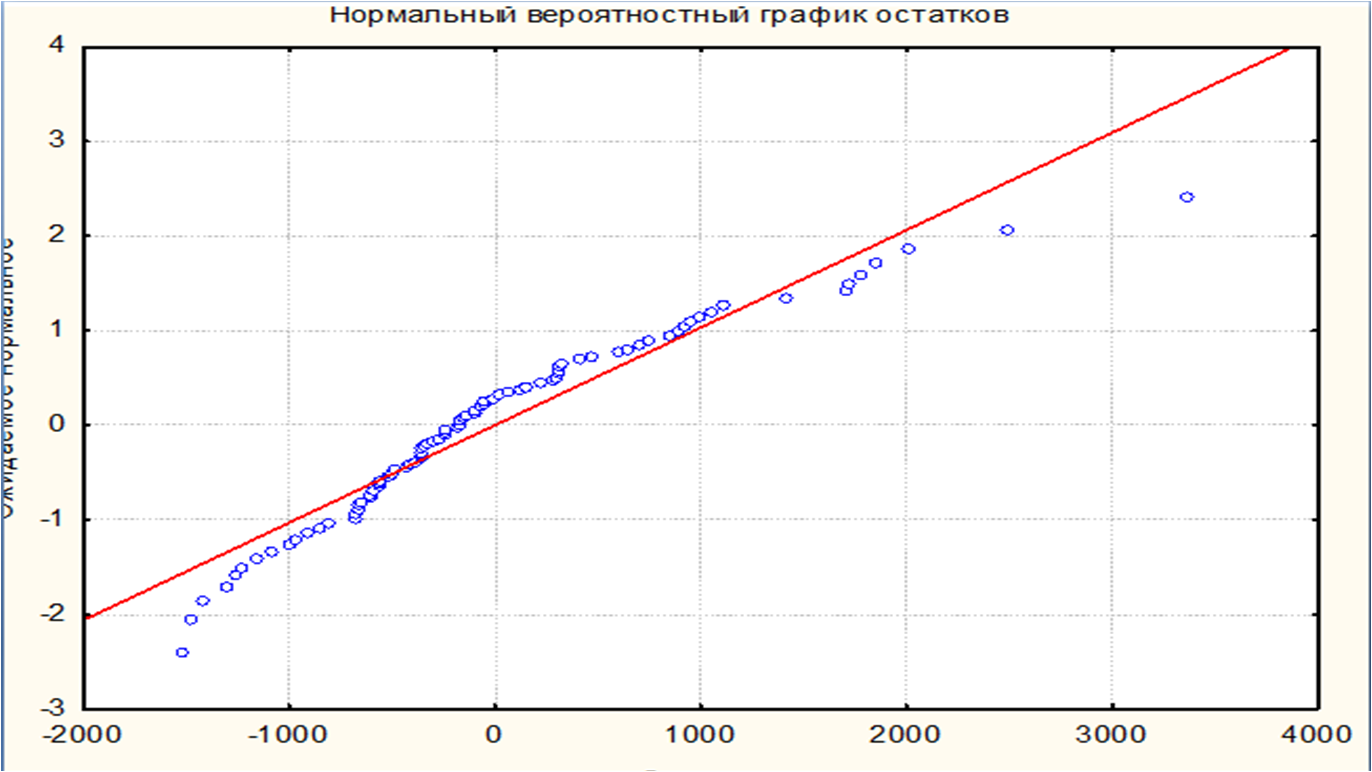
О нормальности остатков можно судить по вероятностному графику остатков, который представлен на рисунке 4.

Рисунок 4 – Нормальный вероятностный график остатков

Так как остатки достаточно хорошо ложатся на прямую, то можно говорить о том, что распределение близко к нормальному.

Таким образом можно сделать вывод, что основными факторами влияющими на трудоемкость единицы продукции У являются F1 -  показатели ресурсов предприятия, F2 – показатели выполнения работ, F3 – удельный вес покупных изделий, F4 – фондовооруженность труда.

1. Колемаев В. А.  Эконометрика : учеб.для студентов вузов по специальности 061800 “Мат. методы в экономике” / В. А. Колемаев ; М-во образования РФ, Гос. ун-т упр. – М. : ИНФРА-М, 2014. – 160 с.
2. Крамер, Н.Ш., Путко, Б.А. Эконометрика: Учебник для вузов [Текст]/ Под рек.проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2012. – 311 с.
3. Эконометрика: учет./под ред.. И. И. Елисеевой. – М.: Проспект, 2009. – 228 с.
4. ЕМИСС государственная статистика [Электронный ресурс]. – Режим доступа: http://www.url: https://fedstat.ru/

Все статьи автора «Харисова Алсу Фанисовна»